Пример алгоритма Диффие Хеллман

Откривање теме криптографије јавног кључа мора почети са историјским путем проблема. Вхитфиелд Диффие и Мартин Хеллман су први питали о отвореном начину предаје кључева. То се догодило 1976. године. Публикација је направила прве покушаје да се проблем ријеши. Њихово решење није било без мана, већ је поставило темеље за потпуно другачији начин размишљања у области шифрованог преноса података.

Предуслови за креирање Диффие-Хеллман алгоритма

До овог тренутка, аутентификација и шифровање били су могући само преко заједничког тајног кључа. Са развојем технологије, питање је постало акутније. Ако 10 особа треба да пренесу податке између себе преко несигурних канала, морат ће међусобно размјењивати лозинке. Овај задатак изгледа стварно. Чак и са потребом да их ажурирате. Уосталом, за 10 пријатеља ће вам требати само 45 тајних кључева. А ако ће контакти бити 100? Требат ће 4950 лозинки. Ситуација расте као снег.

Главно постигнуће Дифија и Хелмана било је исправно формулисање питања и генијални одговор на њега. Предложили су да се подаци могу енкриптовати на један начин и дешифровати у другом. То јест, имају два кључа. Онај који се користи за енкрипцију може бити остављен отворен. Према томе, свака особа може да шифрује поруку, али само власници другог тајног кључа могу да је дешифрују. Али како имплементирати алгоритам за пренос таквог кључа? Научници су били у стању да делимично и дају одговор.

Кратка математика: групе

Диффие-Хеллманов алгоритам или протокол (даље ДХ) ради уз помоћ простих бројева. Нека је довољно велики број који припада скупу прости бројеви. Алгоритам укључује употребу више од 250-500 бајтова. Нека је Да мултипликативна група остатка прстенова по модулу а, који ће бити коришћен Диффие-Хеллмановим алгоритмом шифровања. Састоји се од скупа бројева 1, ..., а-1.

Узмите неки елемент б из групе З _а размотрите бесконачну секвенцу 1, б, б ² , б ³ , б ⁴ , ... Из чињенице да је група З _а по дефиницији коначни скуп, пре или касније разматрана секвенца {б} ће почети да се понавља. Поставите б ^и = б ^ј (и <ј).

Сада дијелимо сваки дио једнакости са б ^и (модуло а) и добијемо б ^ји = 1. То значи да постоји број к = ји за који је б ^к = 1 (мод а) истинит. Најмањи к за који ова једнакост држи се зове редослед б. Да би се избегла конфузија са другом специјалном литературом, стандардна математичка нотација се користи за објашњење Диффие-Хеллмановог система.

Тако, подижући број б, који се назива генерирајући елемент, на снагу, добијамо низ бројева (сет) 1, ..., б ^к-1 . Број елемената у овом скупу је тачно к.

Својство множења модуло а каже да постоји најмање један број б који генерише све елементе групе З * _а . Другим ријечима, постоји број за који је к = а - 1 истинит.Ово својство нам омогућава да представимо бројеве групе З * _а у облику 1, б, б ² , ... б ^а-2 . Такав број б се назива примитивни број групе.

У наставку, из групних знакова је лако доказати да је скуп који је генерисан бројем б такође и сама група и насљеђује сва својства група. Другим речима, операције унутар генерисане групе или подгрупе могу бити изведене на потпуно исти начин као у групи модуло а.

Размотрите изјаву. За било који елемент б, његов ред је делилац а-1. Лако је показати. Нека је а = 7. Број б = 3 је примитиван, пошто 1, ..., б ⁵ = 1, 3, 2, 6, 4, 5. Онда ће број х = 2 генерисати подгрупу 1, ..., х ² = 1 , 2, 4, пошто х ³ = 2 ³ мод 7 = 1. х = 6 генерише подгрупу 1, 6. Величина група је 3 и 2, респективно. Очигледно, то су дивизори броја а-1 = 6.

Први ДХ алгоритам

У оригиналној верзији, алгоритам је радио на следећи начин. Велики број а се бира из скупа једноставног и примитивног елемента б који генерише З * _а . Оба броја а и б представљају јавни кључ, они су познати свима, укључујући и нападаче. Како онда сакрити поруке?

Управо у том кораку Диффие и Хеллман су дошли до врло генијалног потеза. Претпоставимо да имамо две особе које међусобно комуницирају: А и Б. Прво, А бира случајни број к од З * _а , што је еквивалентно избору броја из {1, ..., а-1}. Затим израчунава вредност користећи формулу (б ^к мод а) и шаље је Б. Наизменично, Б бира одређени број и из истог скупа, израчунава вредност (б ^и мод а) и шаље резултат назад А.

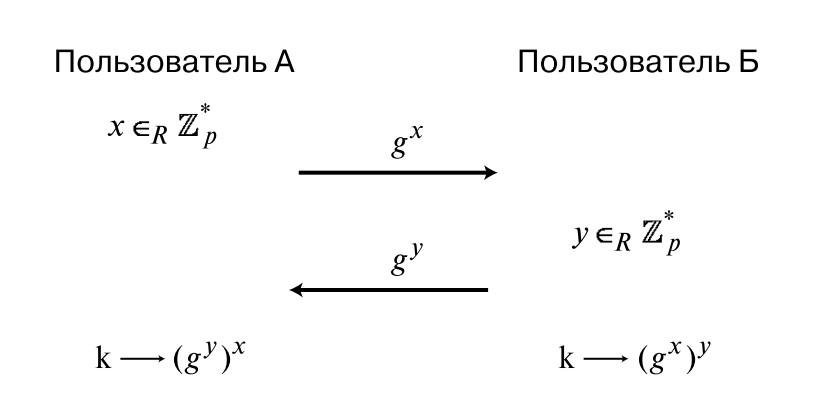
На тако лукав начин, испада да тајни кључ изгледа б ^ки . Због својства степена, који каже г ^ки = (г ^и ) ^к , саговорник А може израчунати жељену вриједност и дешифрирати информације које су му послане. И на исти начин, ову вредност израчунава саговорник Б. Дакле, оба имају исти тајни кључ.

Који проблеми имају уљези са овом размјеном информација? Он може пресрести бројеве г ^к и г ^и . Чак и са знањем јавних кључева, проблем израчунавања г ^ки није тривијалан, т. Пошто не постоји ефикасан алгоритам за проналажење жељене вредности у дистрибуцији Диффие-Хеллманових кључева. Овај проблем је познат као проблем израчунавања дискретног логаритма.

Медијаторски напад

Једна од слабости примарног Диффие-Хеллмановог алгоритма је његова рањивост у односу на посредничке нападе. Шта то значи? Саговорник А зна да комуницира са одређеним лицем, али конкретно с ким - нема појма. Тако нападач може продријети у пренос информација и опонашати суговорника Б када комуницира са А, и обрнуто. Нико од њих неће моћи да посумња да нешто није у реду.

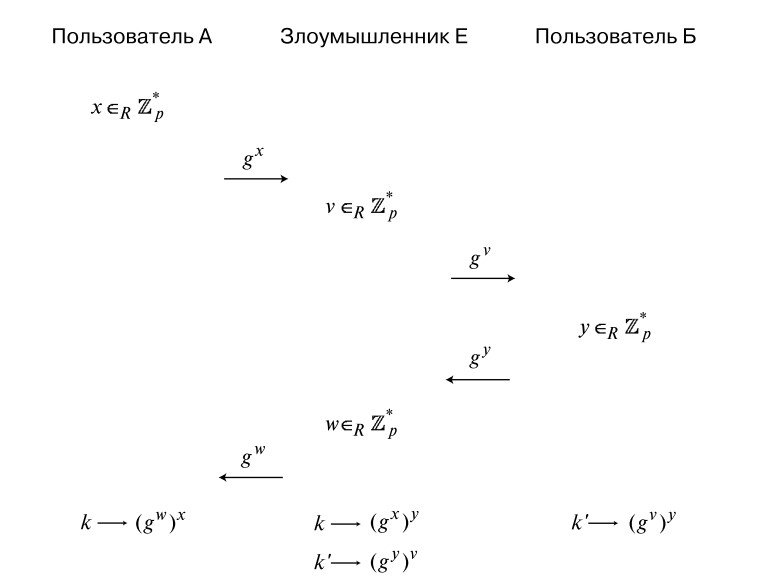
Постоји само једна област коришћења у којој су искључени напади на Диффие-Хеллманов алгоритам. Ово је телефонски и видео позив. Овде, саговорници су у стању да се познају, тако да посредник неће моћи да продре.

Замке

Поред напада посредника, ДХ протокол садржи и низ других проблема. На пример, један од недостатака је случај када примитив није примитиван. Тада генерише само подгрупу. Због сужавања броја могућих опција, нападач отвара могућност њихове претраге.

Проблеми због овог недостатка могу се избјећи ако сваки од саговорника провјери јесу ли бројеви а и б исправни прије почетка размјене података. То јест, а је прост број и б је примитиван. Међутим, када је ријеч о сигурности кроз имплементацију одређених униформних корака, корисници их често игнорирају.

Други озбиљан проблем настаје на основу подгрупа по модулу а. Ако нападач одлучи да промијени г ^к на 1 како би му олакшао прислушкивање, корисници га могу лако открити провјером броја за утакмицу. Међутим, ако замијени кључ с ниским бројем налога, корисници неће моћи ништа посумњати. Пошто ће број елемената у сету са ниским редоследом бити мали, нападач ће морати да издвоји мали број опција за декодирање.

Поузданост простих бројева

ДХ алгоритам користи велики и поуздан број многих једноставних. Како да га изаберете? Ми анализирамо кораке.

1. Користећи формулу а = 2к + 1, изаберите бројеве а и к тако да су једноставни.
2. Из скупа 1, ..., а-1, искључимо 1 и а-1.
3. Узмите случајни број к из сета који остаје после другог корака и пронађите вредност б = к ² (мод а).
4. Уверите се да б није једнак 1 или а-1. Ако је б једнак једној од забрањених вриједности, треба одабрати други к. И поновите операцију.

Скуп (а, к, б) који се добије на овај начин може се сматрати довољним за употребу у Диффие-Хеллман алгоритму размене кључева. Сходно томе, прималац поруке такође треба да провери вредност, која мора бити снага б, и проверити (на пример, функцију Легендре симбола) да пада у скуп који је генерисан бројем б.

Коришћење подгрупа

Главни недостатак горе наведеног алгоритма је недовољна ефикасност. Под претпоставком да је дужина простог броја а н бита, онда је к н-1 бита. Испоставља се да ће сви степени бити н-1 дуги. Онда операција експонентирање у просјеку ће се састојати од 3н / 2 множења мод а. Ово је велики процес.

Да би се носили са овим проблемом, одлучено је да се користе мање подгрупе. Какав је резултат у овом случају? Ако се број а састоји од 2000 бита, тада је потребно 3000 операција множења за израчунавање б ^к . Кроз употребу подгрупа, овај број се може смањити на ~ 400. Ово значајно повећање ефикасности алгоритма омогућава његову пуну примену. На пример, алгоритам Диффие-Хеллман са три или више чланова.

Шта треба да буде дужина а

Правилан избор величина параметара Диффие-Хеллман алгоритма је прилично компликован задатак. Уобичајени захтев у свету криптографије је, на пример, услов да нападач треба најмање ^2.128 корака за пробијање у систем. Ако је у симетричним алгоритмима за шифрирање у складу са таквим захтевом прилично лако, у алгоритмима са јавним кључем то је прави проблем. Ако се придржавате горе наведеног захтева, онда дужина а мора да садржи најмање 850 бајтова.

У пракси, ова величина ствара велике проблеме у перформансама у систему, јер операције јавног кључа трају много дуже него, на пример, у симетричном шифровању са 128 или 256 битним кључевима. Како онда бити? Минимална дужина јавног кључа мора почети у 2048 бита. Иако је кључ дужи, то је виши ниво сигурности. Потребно је узети у обзир првенствено перформансе система и његове трошкове. Ако вам дозвољава да користите кључ од 4096 бита, морате то да урадите.

Како се процењује захтевани ниво безбедности?

Величина кључа у симетричном шифровању остаје непромењена (128, 256 бита) током целог живота система, док су величине јавног кључа увек променљиве вредности. Ако морате развити систем који се мора користити 30 година и чувати податке у тајности најмање 20 година након што се систем избаци из употребе, тада величина симетричног кључа за шифровање мора бити довољно велика да заштити систем у наредних 50 година.

Због очигледних проблема са перформансама, због чињенице да Диффие-Хеллман алгоритам шифрира много више операција, захтеви за јавне кључеве се разликују. Она остаје на снази годину дана и штити податке за наредних 20 година, односно користи се укупно 21 годину. Због промјењиве величине, кључ се може мијењати сваке године и стварати све дуже како би се осигурао потребан ниво сигурности.

На пример, најбоље процене показују да кључ са дужином од 256 бајтова може да заштити податке за ~ 20 година, дужина од 384 бајта је 35 година, и са дужином од 512 бајта је 47 година, итд. Потребно је ^2.128 корака да би се испуцао, изведен из сличних процјена. Међутим, ово је само предвиђање, које морате пажљиво поуздати. Можете прилично тачно предвидети развој догађаја за 10 година унапријед, али на 50 - ово је фантастично.

Практичне препоруке

Ево неколико практичних савета о коришћењу ДХ протокола. Изаберите к као прост број од 256 бита. То је минимум који може пружити барем неки адекватан ниво сигурности од напада. За а, изаберите број који би имао облик На + 1, где је Н цео број. О величини броја а речено је раније. Након тога се бира случајни број б и проверава се за неколико услова. Прво, не може бити јединица. Друго, б ^к = 1.

Заузврат, сваки учесник у комуникацији треба да се увери у следеће:

• а и к су прости бројеви, дужина к је 256 бита, дужина п је прилично велика.
• број к је делилац а-1.
• б није једнак 1 и б ^к = 1.

Ове услове треба проверити и уз безусловно поверење у извор.

Закључак

ДХ алгоритам је генијално решење једног од озбиљних проблема и још увек се активно користи у модификованом облику за савремене безбедносне захтеве у различитим протоколима. Диффие-Хеллманов алгоритам, на пример, користи се у неким деловима имплементације ИКЕ протокола. Међутим, његова употреба треба да буде методична и опрезна због присутности очигледних проблема и озбиљних замки.