Како пронаћи праве бројеве?

Бројеви су различити: природни, природни, рационални, целобројни и фракцијски, позитивни и негативни, сложени и једноставни, непарни и парцијални, реални, итд. Из овог чланка можете сазнати који су једноставни бројеви.

Који се бројеви називају енглеска ријеч "симпл"?

Врло често, студенти на једном од најлакших питања математике на први поглед, о томе шта је то прост број, не знају како да одговоре. Често бркају једноставне бројеве са природним бројевима (тј. Бројеве које људи користе приликом бројања ставки, док у неким изворима почињу од нуле, ау другима - од једног). Али то су потпуно две различите ствари. Приме бројеви су природни, односно цели бројеви и позитивни бројеви, који су већи од једног и који имају само 2 природна раздјелника. У овом случају, један од ових делитеља је дани број, а други је један. На пример, три су прости број, пошто није дељив ни на један други број осим на себе и један.

Цомпоунд нумберс

Супротно од примес је спој. Такође су природне, такође више од једне, али немају два, већ већи број разделника. На пример, бројеви 4, 6, 8, 9 итд. Су природни, композитни, али не и прости бројеви. Као што видите, то су углавном парни бројеви, али не сви. Али “два” - парни број и “први број” у низу простих бројева.

Секуенце

Да бисмо направили низ простих бројева, потребно је извршити селекцију из свих природних бројева, узимајући у обзир њихову дефиницију, тј. Морате поступати супротно. Потребно је размотрити сваки од позитивних целих бројева да би се утврдило да ли има више од два делиоца. Хајде да покушамо да направимо серију (секвенцу) која чини прост број. Листа почиње са два, следећа је три, јер је подељена само на себе и на јединице. Размотримо број четири. Има ли раздвајача осим четири и један? Да, овај број је 2. Дакле, четири нису прости број. Пет је такође једноставан (не може се делити са другим бројем осим 1 и 5), али шест је дељиво. Уопштено говорећи, ако пратите све парне бројеве, можете видјети да осим за два, ниједна од њих није једноставна. Одавде закључујемо да чак и бројеви, осим два, нису једноставни. Још једно откриће: сви бројеви који су дељиви на три, осим самог тријаде, било да је паран или непаран, такође нису једноставни (6, 9, 12, 15, 18, 21, 24, 27, итд.). Исто важи и за бројеве који се дијеле на пет и седам. Сви они такође нису једноставни. Да резимирамо. Дакле, све цифре су све одд бројеви осим једног и деветог, а од парног - само “два”. Сама десетине (10, 20, ... 40, итд.) Нису једноставне. Двоцифрене, трознаменкасте и тако даље једноставне бројеве можемо одредити на основу горе наведених принципа: ако немају друге делитеље осим себе и оне.

Теорије о својствима простих бројева

Постоји наука која проучава својства целих бројева, укључујући примес. Ово је грана математике, која се зове највиша. Поред својстава целих бројева, она се такође бави алгебарским, трансценденталним бројевима, као и функцијама различитог порекла које су повезане са аритметиком ових бројева. У овим студијама, поред елементарних и алгебарских метода, користе се и аналитички и геометријски. Наиме, проучавање простих бројева укључених у теорију бројева.

Првобитни бројеви су "грађевни блокови" природних бројева.

У аритметици постоји теорема, која се назива главна. Према њему, сваки природни број, осим једног, може се представити као производ чији су фактори једноставни бројеви, а редослијед редослиједа фактора је јединствен, то значи да је начин представљања јединствен. То се назива декомпозиција природног броја на просте факторе. Постоји још једно име за овај процес - факторизација бројева. Полазећи од тога, једноставни бројеви се могу назвати „грађевински материјал“, „блокови“ за изградњу природних бројева.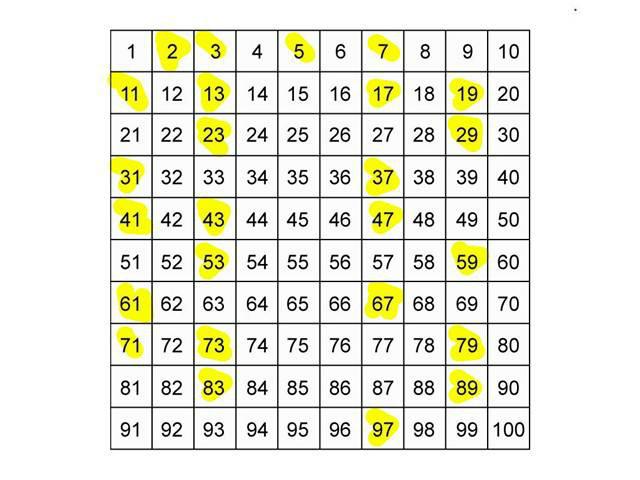

Тражите праве бројеве. Тестови једноставности

Многи научници различитих времена покушали су да пронађу неке принципе (системе) за проналажење листе простих бројева. Наука познаје системе који се зову Аткин сито, Сундартам сито и Ератостеново сито. Међутим, они не дају никакве значајне резултате, а једноставна провјера се користи за проналажење примеса. Такође, математичари су креирали алгоритме. Називају се тестови једноставности. На пример, постоји тест који су развили Рабин и Миллер. Користе га криптографи. Постоји и Каиал-Агравал-Саскен тест. Међутим, упркос његовој довољној прецизности, врло је тешко израчунати, што умањује његову практичну вриједност.

Да ли скуп простих бројева има ограничење?

Чињеница да је скуп једноставних је бесконачност, написао је у књизи "Принципи" древни грчки учењак Еуклид. Рекао је ово: „Замислимо на тренутак да примес има границу. Онда их помножимо једни с другима и додамо један производу. Број који се добије као резултат ових једноставних акција не може се поделити на један од бројних простих бројева, јер ће увек бити један у остатку. А то значи да постоји неки други број који још није укључен у листу простих бројева. Дакле, наша претпоставка није истинита, и овај скуп не може имати ограничење. Поред доказа о Еуклиду, постоји и модернија формула коју је дао швајцарски математичар из осамнаестог века Леонард Еулер. Према њему, инверзна сума од првих н бројева расте без граница како број н расте. Али формула теореме о расподели простих бројева: (н) расте као н / лн (н).

Који је највећи прост број?

Исти Леонард Еулер је успео да пронађе највећи премијер за своје време. Ово је 2 ³¹ - 1 = 2147483647. Међутим, до 2013, израчуната је друга најпрецизнија у листи простих бројева, 2 ^57885161 - 1, која се зове Мерсеннов број. Садржи око 17 милиона децималних цифара. Као што можете да видите, број који су пронашли научници из осамнаестог века је неколико пута мањи од овог. То је морало да буде тако, јер је Еулер ручно вршио ову калкулацију, али је наш рачунар вероватно помогао наш савремени. Штавише, овај број је стечен на математичком факултету на једном од америчких факултета. Бројеви, названи по овом научнику, пролазе кроз Луке-Лемере тест једноставности. Међутим, наука не жели ту да се заустави. Елецтрониц Фронтиер Фоундатион, која је основана 1990. године у Сједињеним Америчким Државама (ЕФФ), именовала је новчану награду за проналажење великих простих бројева. И ако је до 2013. награда била ослоњена на оне научнике који би их пронашли између 1 и 10 милиона децималних бројева, данас је та бројка достигла од 100 милиона до 1 милијарде. Величина награде креће се од 150 до 250 хиљада америчких долара.

Имена специјалних примеса

Ти бројеви који су пронађени захваљујући алгоритмима које је створио један или други научник и који су прошли тест једноставности, називају се посебним. Ево неких од њих:

1. Мерссен.

2. Воода.

3. Фарма.

4. Цуллен.

5. Прота.

6. Миллс ет ал.

Једноставност ових бројева, названа по наведеним научницима, утврђује се коришћењем следећих тестова:

1. Луц-Лемер.

2. Пепин.

3. Ризел.

4. Биллхарт - Лемера - Селфридге, итд.

Модерна наука се не зауставља на томе, и вероватно је да ће у блиској будућности свијет знати имена оних који би могли добити награду од 250.000 долара, проналазећи највећи премијерни број.