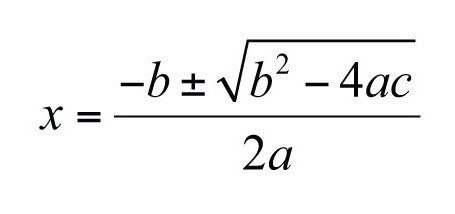Како пронаћи корен једнаџбе: линеарно, квадратно, кубично?

Једнаџбе у математици су једнако важне као глаголи на руском. Без способности да пронађе корен једначине, тешко је тврдити да је ученик савладао курс алгебре. Поред тога, за сваку од њихових врста постоје њихова специфична решења.

Шта је то?

Једнаџба је два произвољна израза који садрже варијабле са знаком једнакости између њих. Штавише, број непознатих количина може бити произвољан. Минимални број је један.

Решење је да се сазна да ли постоји корен једначине. То је број који га претвара у исправну једнакост. Ако није, онда је одговор изјава да "нема корена". Али може бити супротно када је одговор мноштво бројева.

Какве једначине постоје?

Линеар. Садржи варијаблу чији је степен једнак једном.

• Скуаре. Варијабла стоји са снагом од 2, или трансформација резултира у таквом степену.
• Једнаџба највишег степена.
• Фракционо рационално. Када је варијабла у именитељу фракције.
• Витх модуле.
• Ирратионал То јест, онај који садржи алгебарски корен.

Како се решава линеарна једначина?

Она је главна. У том погледу сви други желе да воде. Пошто је лако пронаћи корен једначине.

• Прво, потребно је извршити могуће трансформације, односно проширити заграде и дати сличне изразе.
• Преместите све мономиале са променљивом на леву страну једначине, остављајући слободне термине на десној страни.
• Донесите сличне изразе у сваком дијелу једнаџбе које треба ријешити.
• У насталој једнакости у његовој левој половини биће производ коефицијента и варијабле, ау десној половини ће бити број.
• Остаје да се пронађе корен једначине, дељење броја на десно, са коефицијентом испред непознатог.

Како пронаћи корене квадратне једнаџбе?

Прво, она мора бити сведена на стандардни образац, тј. Све заграде треба да се отворе, слични термини треба да се унесу, и сви мономали треба да се померају на леву страну. Са десне стране једнакости, треба да остане само нула.

• Користите дискриминантну формулу. Квадратирање коефицијента пре непознатог са степеном "1". Помножите слободни мономиј и број испред варијабле у квадрату са бројем 4. Одузмите производ од резултујућег квадрата.
• Процијените вриједност дискриминанта. Негативно је - одлука је завршена, јер нема корена. Једнак нули - одговор је један број. Позитивна - двије вриједности варијабле.

• 

  Пронађите два корена једначине према формули у којој скуаре роот од дискриминанта мора се одузети или додати негативном коефицијенту варијабле у првом степену. Тада поделите са двоструким коефицијентом према квадрату непознатог. (У случају једнакости дискриминантног, нула ће бити потребно додати или одузети, тако да ће се два корена подударати.)

Како ријешити кубичну једнаџбу?

Прво пронађите корен једначине к. Она се одређује методом селекције из бројева који су делиоци слободног термина. Овај метод је погодан за разматрање специфичног примера. Нека је једнаџба: к ³ - 3к ² - 4к + 12 = 0.

Његов слободни термин је 12. Онда ће дивизори који треба да буду проверени бити позитивни и негативни бројеви: 1, 2, 3, 4, 6 и 12. Претрага се може обавити на броју 2. Она даје истинску једнакост у једначини. То значи да се његова лева страна покаже нулом. Дакле, број 2 је први цубиц роот једначине.

Сада морате поделити оригиналну једначину разликом између варијабле и првог корена. У конкретном примеру, ово је (к - 2). Једноставна трансформација доводи до таквог факторизације нумератора: (к - 2) (к + 2) (к - 3). Исти фактори нумератора и имениоца су смањени, а преостала два заграда у приказу дају једноставну квадратну једнаџбу: к ² - к - 6 = 0.

Овде проналазимо два корена једначине према принципу описаном у претходном одељку. То су бројеви: 3 и -2.

Дакле, конкретна кубична једначина има три корена: 2, -2 и 3.

Како се решавају системи линеарне једначине?

Овде је предложен метод за елиминисање непознатих. Она се састоји у изражавању једне непознате кроз другу у једној једнаџби и замјеном тог израза у другу. Штавише, решење система двеју једначина са две непознате је увек пар променљивих.

Ако су варијабле у њима означене словима к ₁ и к ₂ , онда можемо извести из прве једначине, на пример, к ₂ . Затим се замењује у други. Проводи се неопходна трансформација: откривање заграда и присила сличних чланова. Испоставља се једноставна линеарна једначина, чији је корен лако израчунати.

Сада се вратите на прву једначину и пронађите корен једнаџбе к ₂ , користећи добијену једначину. Ова два броја су одговор.

Једноставни савети

Да бисте били сигурни у одговор на примљени одговор, препоручујемо да увек извршите чек. Није потребно писати.

Ако је једна једначина решена, онда сваки њен корен мора бити замењен првобитном једнакошћу и добити исте бројеве у оба дела. Све се спојило - права одлука.

Приликом рада са системом, потребно је заменити корене у сваком решењу и извршити све могуће акције. Испоставља се исправна једнакост? Дакле, одлука је тачна.