Како пронаћи волумен цилиндра: формуле и проблем
Питање како пронаћи волумен цилиндра може настати не само од ученика. На крају крајева, овај облик има, на пример, тигањ, чији је капацитет понекад хитно потребан да би се то сазнало. Тада вам је потребно познавање посебне формуле.
Шта треба да знате о цилиндру?
Геометријско тело о којем говоримо је формирано ротирањем правоугаоника око једне његове стране, и увек ће бити равно. То значи да је угао између генератора цилиндра и његове базе у овом случају 90 степени. Ако овај једноставни покрет не успе, а угао више није 90 степени, онда говоримо о нагнутом цилиндру.
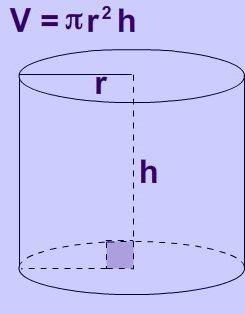
Какав год да је изглед тела, још увек морате да знате како да нађете запремина цилиндра. Али прво морате одлучити о неким теоријским подацима.
Како се зову поједини елементи цилиндра и шта се о њима зна?
Сегменти који се спајају у пару одговарајућим тачкама на две базе називају се генератори. У сваком цилиндру су једнаке и паралелне једна са другом. Ако је равна, онда се дужина генератрика подудара са висином тела.
Ad
Кружница или елипса могу лежати у бази, затим ће цилиндар бити кружни или елиптични, респективно. У формулама, ова чињеница ће се морати узети у обзир. Зато што се најчешће дају за кружни цилиндар. У елиптичком, пре израчунавања запремине цилиндра, мораћете да сазнате по којој формули одредите површину овала.
Формуле запремине за равне и косе цилиндре
У даљем тексту се узимају такве ознаке.
| Леттер десигнатион | математичка количина |
| В | волумен |
| С | основна област |
| х | висина |
| р | радијус круга |
| л | генератрик ленгтх |
| α | угао између генератора и базе |
У сваком случају, потребна вам је формула у којој се висина тела множи са површином базе. Изгледа овако:
В = Сх
Ако желите да сазнате како да нађете запремину цилиндра равно, онда се овде дужина дужине потпуно поклапа са генератором. Основа је најчешће круг, затим се његова површина израчунава по формули:
С = πр 2 .
Када је проблем око елиптичног цилиндра, потребна је следећа формула за подручје базе:
С = π аб , овде слова а и б означавају мање и главне полуосовине овала.
Приликом решавања проблема на нагнутом цилиндру потребно је увести неке додатке у формулу. На пример, ако висина није позната, али то је питање генератора и угла између њега и базе. Тада слово х треба да буде замењено таквим изразом:
Ad
х = л * син α .
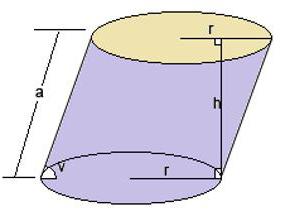
Шта ако требате одредити обим у пракси?
У проблемима, вредности угла или висине код генератора су обично већ познате. И можда неки други елементи кроз које се могу наћи. У животу морате сами да урадите мерења.
Онда се питање како одредити запремину цилиндра своди на правилно мерење његове висине и радијуса. Да бисте то урадили, требат ће вам: равнало, оловка и правокутни лист папира.
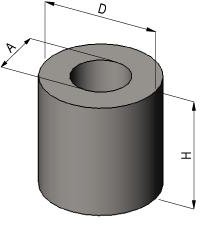
Најчешће у свакодневном животу окружујемо правим кружним цилиндрима. Мерење њихове висине обично није тешко. Потребно је само да причврстите равнало на страну и измерите растојање од дна до врха тела. То ће бити висина - х.
Са радијусом круга, све није тако лако. Морамо запамтити мало геометрије. Овде вам је потребан лист папира са правим углом и оловком.
Шта даје теорија геометрије? Око правоугаони троугао Можете описати круг. Штавише, његов прави угао ће бити на њему, а хипотенуза ће се подударати са пречником.
Треба да узмете лист папира и ставите га тако да прави угао додирује ивицу базе. Тада ће његове две стране, које формирају овај угао, пресећи круг у неким тачкама. На тим местима морате направити ознаке. На њима да проведу сегмент. То ће бити хипотенуза и жељени пречник базе цилиндра.
Ad
Како пронаћи волумен цилиндра, у нашем случају? Формула садржи радијус. Она је једнака половини пречника. То јест, дужина резултирајућег сегмента треба поделити на два дела.
Остаје само замјена резултата мјерења у формули за волумен и бројање. И узмите у обзир да је одговор у цм3. Ако се обим треба знати у кубним метрима, онда ће број морати да се подели са милион. Да би добили волумен у литрама, дјелитељ ће бити тисућу.
Задатак
Цондитион Два цилиндра. Висина прва два пута у другом. Радијус другог је двоструко већи од првог. Потребно је сазнати колико пута је волумен првог цилиндра већи или мањи од волумена другог.
Одлука. Прво морате да унесете нотацију. Нека висина и радијус првог тела буду индекс 1, а други - 2.
Сада можете записати податке у вредности услова у облику израза:
х 1 = 2х 2 и р 2 = 2р 1 .
Формуле за запремине оба цилиндра ће изгледати овако:
в 1 = π р 1 2 х 1 и в 2 = π р 2 2 х 2 .
Задатак захтева да нађете:
в 1 : в 2 = (π р 1 2 х 1 ): (π р 2 2 х 2 ).
Након смањења π и замене х 1 и р 2 са унесеним изразима, испада:
в 1 : в 2 = (р 1 2 2х 2 ): (4р 1 2 х 2 ).
То је, в 1 : в 2 = 1: 2. То значи да је запремина првог цилиндра два пута мања.
Одговор је. в 1 = в 2 : 2.