Клеин боца: својства и употреба

Клеинова боца је дводимензионална многострукост, одређена не-оријентисана површина. Први пут га је описао немачки математичар Клеин 1882. године. Ако исечете Клеин боцу дуж њене осе симетрије на пола на једнаке делове, резултат ће бити Мобиусова трака. Сам назив, највероватније, потиче од погрешног превода са немачке речи Флацхе - површина. Пишући, ова ријеч је близу ријечи Фласцхе - боца. У будућности, ово име се у овој верзији враћа на њемачки језик.

Сфера изнутра

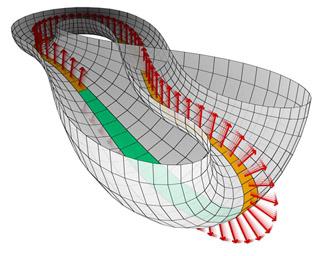
Мобиус Тапе, Клеин боца и хептахедрон - све је то потпуно статички дизајн са површинама које су изнутра према ван. У 20. веку тополози су почели да решавају проблеме динамичне природе, а прва од њих била је инверзија сфере. За разлику од горњих фигура, површина сфере је оријентисана. Његова унутрашња страна може бити обојена плавом, а спољашња - црвена. Ако, након таквог бојења површина, измјенимо јужни и сјеверни пол кугле на мјестима, помичући их дуж оси повезивања, кугла ће се окренути изнутра према ван тако да њена вањска површина постане плава, а унутрашња површина црвена. Преклапање се формира дуж читавог опсега екватора. Али то није све: када полови пролазе уздуж оси највећи део пута, а спољашња површина сфере мења боју из црвене у плаву, а затим дужина екватора створиће се тороидна површина, обојена споља црвеном бојом. Сходно томе, сфера која је испољена на пола показује још један интересантан ефекат у топологији - преплитање спољашњег и унутрашњег простора, јер се обе површине испољавају споља.

Како направити модел бочице Клеин

Прво морате узети боцу са рупама у зиду и на дну и повући врат, савити га и проћи кроз рупу у зиду. Ако изградите модел праве бочице у четверодимензионалном простору, онда нема потребе за рупом у зиду. Али без њега се не може радити ако је модел изграђен у тродимензионалном еуклидском простору (Р3). Затим се врат мора причврстити за рупу на дну. Клеин боца, за разлику од обичног стакла, нема „ивицу“ где се површина нагло завршава. Ако га упоредимо са балоном, онда пут од унутрашњости ка споља пролази без преласка површине. Дакле, у стварности објекат нема ни унутрашњу ни спољну површину.

Клеин боца: примена и својства

Овај објекат, као и Мобиусова трака, је дводимензионална диференцијабилна не-оријентисана многозначница. Али, за разлику од врпце, Клеин боца је компактна многострука без ивице. Ако залепите два Мобиус обруча дуж ивица, добићете боцу Клеина. Али то се не може урадити у уобичајеном простору (Р3) без стварања само-раскрснице. Клеин боца се може уронити само у њу тродимензионални простор али истовремено може бити уграђен у четверодимензионални простор. Овај објекат има хроматски број површина од шест.