Ротациона кретања и угаона брзина крутине

У овом чланку ћемо говорити о физичким величинама које карактеришу ротационо кретање тела: угаона брзина, угаоно померање, угловно убрзање и момент сила.

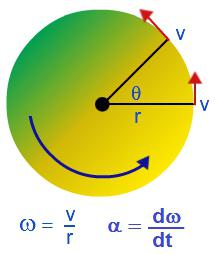
Круто тело је скуп чврсто повезаних материјалних тачака. Када се чврсто тело окреће око било које осе, појединачне материјалне тачке из којих се додаје крећу се по круговима различитих полупречника.

На пример, током одређеног временског периода, током којег тело прави једну револуцију, одвојене материјалне тачке које сачињавају чврсто тело пролазе различите путеве, тако да ће одвојене тачке имати различите линеарне брзине. Описати ротацију крутине користећи линеарне брзине појединца материјалне тачке - тешко.

Ангулар дисплацемент

Међутим, анализирајући кретање појединачних материјалних тачака, може се утврдити да се у истом временском периоду сви окрећу око осе под истим углом. То јест, да би се описала ротација чврстог материјала, погодно је користити такву физичку величину као кутни помак:

φ = φ (т).

Угаона брзина и угловно убрзање

Ротационо кретање се може карактерисати угаоном брзином: ω = = / ∆т.

Угаона брзина карактерише брзину ротације тела и једнака је односу промене угла ротације према времену у коме је дошло. Измерена у радијанима у секунди: [ω] = рад / с.

Угаона брзина ротације је повезана са линеарном брзином следећом релацијом: в = Рω, где је Р полупречник круга уз који се тело креће.

Ротациони покрет тело се одликује другом физичком величином - угаоном убрзањем, које је једнако односу промене угаоне брзине на време током кога је дошло до тога: ε = /ω / .т. Јединица за мерење угловног убрзања: [ε] = рад / с ² .

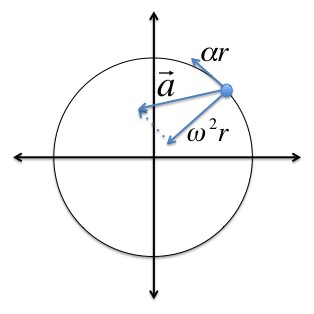
Угаона брзина и угаоно убрзање су псеудовектори, чији смер зависи од правца ротације. Може се одредити правилом десног вијка.

Јединствено ротационо кретање

Уједначено ротационо кретање се изводи са константном кутном брзином и описује се следећим једначинама: ε = 0, ω = цонст, φ = + ₀ + ωт, где је ис ₀ почетна вредност угла ротације.

Једнако убрзано ротационо кретање

Једнако убрзано ротационо кретање јавља се са константним угаоним убрзањем и описује се следећим једначинама: ε = цонст, ω = ω ₀ + εт, φ = + ₀ + ω ₀ т + εт 2/2.

За време ротације чврстог материјала центрипетално убрзање свака тачка овог тела може се наћи на следећи начин :. _ц = в ² / Р = (ωР) ² / Р = ω ² Р.

Када се ротација чврстог тела убрза, тангенцијално убрзање њених тачака може се наћи формулом: ɑ _т = /В / =т = ∆ (ωР) / =т = Р (/ω / )т) = Рε.

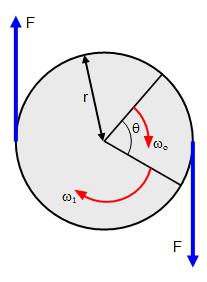
Тренутак снаге

Ако се, с обзиром на физички проблем, не бавимо материјалном тачком, већ чврстим тијелом, онда се дјеловање више сила на њега примјењује на различите точке овог тијела не може се свести на дјеловање једне силе. У овом случају, размотрите тренутак сила.

Момент силе се назива производом силе на рамену. Ово је векторска величина, и налази се по формули: М = РФсинα, где је α угао између вектора Р и Ф. Ако постоји неколико момената сила које дјелују на тијело, тада се њихово дјеловање може замијенити њиховим резултантним, векторским збројем тих момената: М = М ₁ + М ₂ + ... + М _н .

Експерименти и искуства показују да се под дејством тренутка силе мења угаона брзина тела, тј. Тело има угаоно убрзање. Утврдимо како угаоно убрзање материјалне тачке (скуп материјалних тачака) зависи од примењеног обртног момента: Ф = мɑ, РФ = Рма = Р ² мβ, β = М / мР ² = М / И, где је И = мР ² момент инерције материјала бодова. Имајте на уму да момент инерције тела зависи како од масе тела тако и од локације те масе у односу на ос ротације.

Примери решавања проблема

Задатак 1. Ротор центрифуге чини 2 • 10 ⁴ о / мин. Након што се мотор искључи, његова ротација се зауставља након 8 минута. Нађите угаоно убрзање, као и број обртаја које ротор прави од тренутка када се мотор искључи док се не заустави, с обзиром да је кретање ротора једнолико убрзано.

Решење

Нађимо угаоно убрзање, узимајући у обзир да је угаона брзина са равномерно убрзаним кретањем описана једнаџбом: ω (т) = ω ₀ - εт.

Дакле, с обзиром да је на крају кретања брзина нула, налазимо: ε = ω ₀ / т = 2πн / т.

Преносом ових задатака на СИ јединицу јединица (н = 333 о / с; т = 480 с) добијамо: ε = 2π333 / 480 = 4.36 (рад / с ² ).

Угао ротације ротора центрифуге током времена т ће бити: φ (т) = + ₀ + ω ₀ т + εт 2/2. И читајући израз за кутно убрзање и чињеницу да φ ₀ = 0 , налазимо: φ (т) = ω ₀ т / 2 = πнт.

Број обртаја ротора за то време ће бити: Н = т (т) / 2π = πнт / 2π = нт = 8 • 10 ⁴ (вол.).

Одговор: кутно убрзање износи 4,36 рад / с ² ; број обртаја које је направио ротор од тренутка када је мотор искључен док се потпуно не заустави износи 8 • 10 ⁴ о / мин.

Задатак 2. Диск са масом од 1 кг и радијусом од 20 цм ротира са фреквенцијом од 120 о / мин. за минут. Под дејством кочионог уређаја на ивици диска је почело да делује сила трења 10 Н. Нађите времена да зауставите диск, након што је почела да делује на снагу трења.

Решење

Пронађите кочни момент који делује на диск: М = РФ.

Нађите кутно убрзање диска: ε = М / И = ФР / мР ² = Ф / мР.

Нађите време за које ће се диск зауставити: т = ω ₀ / ε , где је ω ₀ почетна угаона брзина диска, која је једнака 2πв.

Израчунавамо: т = 2πв / ε = 2πвмР / Ф = 6.28 • 2 • 1 • 0.2 / 10 = 2.5 (с).

Одговор: време заустављања је 2,5 секунде.