Типови троуглова. Триангле англес

Најједноставнији полигон који се проучава у школи је троугао. То је за ученике разумљивије и има мање потешкоћа. Упркос чињеници да постоје различити типови троуглова, који имају посебна својства.

Који облик се назива троугао?

Формирана од три тачке и сегмената. Први се назива вертицес, а друга страна. Штавише, сва три сегмента треба да буду повезана у облику углова између њих. Отуда и име фигуре "троугао".

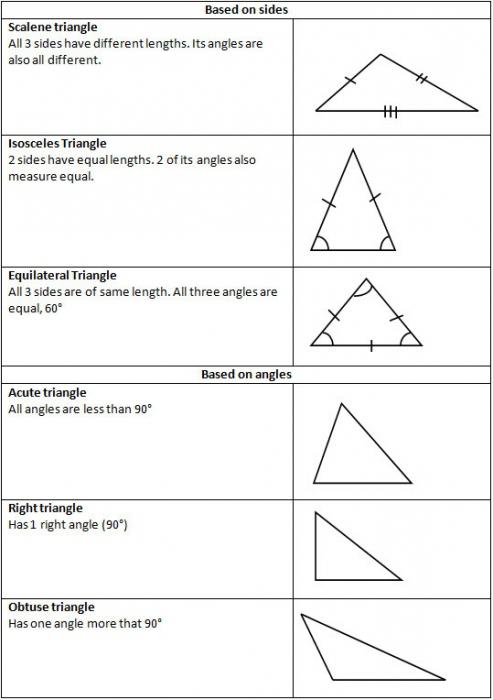
Разлике у називима углова

Пошто могу бити оштри, тупи и равни, онда се типови троуглова одређују тим именима. Према томе, постоје три групе таквих бројки.

• Први. Ако су сви углови троугла акутни, онда ће имати име акутног угла. Све је логично.

• Други. Један од углова је туп, што значи трокутасти угао. Једноставно нема мјеста.

• Треће. Постоји угао од 90 степени, који се назива раван. Троугао постаје правоугаони.

Разлике у именима на странама

У зависности од карактеристика страна, ови типови троуглова се разликују:

• општи случај је свестран, у коме све стране имају произвољну дужину;

• једнакокраке, од којих две стране имају исте нумеричке вредности;

• једнакостраним, дужине свих његових страна су исте.

Ако задатак не специфицира одређени тип троугла, онда морате нацртати произвољну. У којима су сви углови оштри, а странице имају различите дужине.

Својства која су заједничка свим троугловима

1. Ако збројите све углове троугла, добићете број једнак 180º. И без обзира на то како изгледа. Ово правило је увек валидно.
2. Нумеричка вредност било које стране троугла је мања од друге две. У исто време, то је више од њихове разлике.
3. Сваки спољашњи угао има вредност која се добија додавањем два унутрашња, а не суседна. Штавише, то је увек више од унутрашњег, поред њега.
4. Насупрот мањој страни троугла је увек најмањи угао. Насупрот томе, ако је страна велика, онда ће угао бити највећи.

Ова својства су увек валидна, без обзира на врсту троуглова који се разматрају у проблемима. Сви остали слиједе специфичне особине.

Својства једнакокрачног троугла

• Углови који се налазе поред базе су једнаки.
• Висина која се држи на бази је такође средња и симетрала.
• Висине, медијани и симетрале које су изграђене на странама троугла су једнаке једна другој.

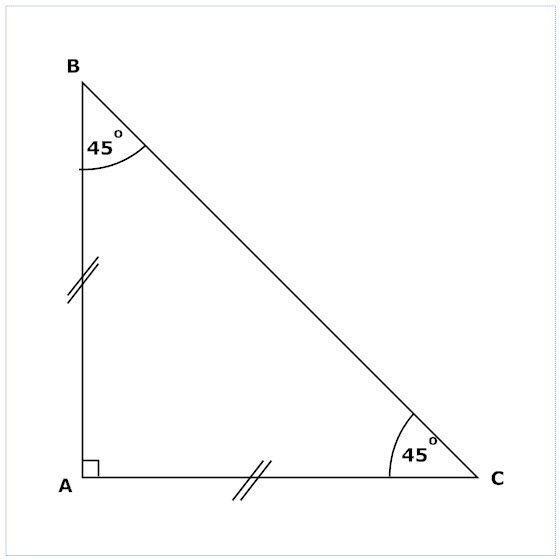
Својства једнакостраничног троугла

Ако постоји таква фигура, онда ће све горе описане особине бити истините. Зато што ће једнакостраница увек бити једнакокраке. Али не обрнуто, једнакокрачан троугао неће нужно бити једнакостран.

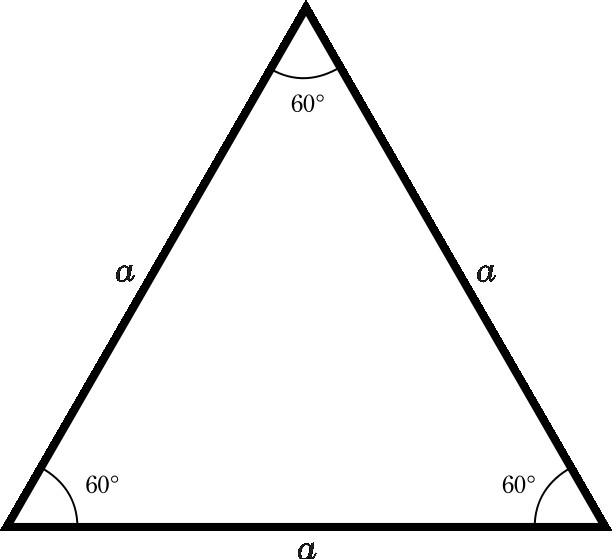
• Сви њени углови су једнаки један другом и имају вредност од 60º.
• Било која средња вредност једнакостраничног троугла је његова висина и симетрала. И сви су једнаки. Да би се одредиле њихове вредности, постоји формула која се састоји од производа странке скуаре роот од 3 подељено са 2.

Својства правог трокута

• Два акутна угла дају укупну вредност од 90º.
• Дужина хипотенузе је увек већа од дужине било које ноге.
• Бројчана вредност медиане која је спроведена до хипотенузе је половина.
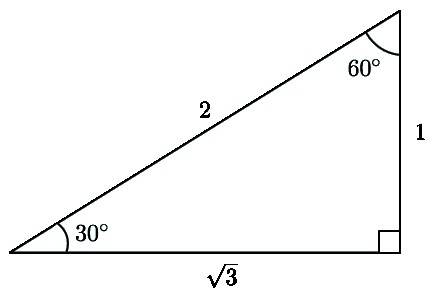
• Иста вредност је једнака нози, ако се налази наспрам угла од 30º.
• Висина, која се извлачи са врха са вредношћу од 90º, има одређену математичку зависност од ногу: 1 / н ² = 1 / а ² + 1 / у ² . Овде: а, ц - ноге, н - висина.

Задаци са различитим типовима троуглова

№1. Даје се једнакокрачан троугао. Њен периметар је познат и износи 90 цм. Као додатни услов: страна је мања од базе за 1,2 пута.

Решење

Вриједност периметра је директно овисна о вриједностима које је потребно пронаћи. Збир свих трију страна ће дати 90 цм, а сада морамо да се присетимо знака троугла, у коме је једнакокрачан. То јест, две стране су једнаке. Можете направити једнаџбу са двије непознанице: 2а + б = 90. Овдје је а страна, у - база.

То је преокрет додатног услова. Након тога, добијена је друга једнаџба: в = 1,2а. Овај израз можете заменити у првом. Испада: 2а + 1.2а = 90. Након трансформација: 3.2а = 90. Одавде а = 28.125 (цм). Сада је лако пронаћи основу. Ово је најбоље урадити из другог услова: ц = 1.2 * 28.125 = 33.75 (цм).

Да бисте проверили, можете додати три вредности: 28.125 * 2 + 33.75 = 90 (цм). Тако је.

Одговор: стране троугла су 28.125 цм, 28.125 цм, 33.75 цм.

№2. Страна једнакостраничног троугла је 12 цм и потребно је израчунати његову висину.

Одлука. Да би се тражио одговор, довољно је да се вратимо на тачку где су описана својства троугла. Ово је формула за проналажење висине, медијана и симетрала једнакостраничног троугла.

н = а * /3 / 2, где је н висина и а страна.

Супституција и прорачун дају следећи резултат: н = 6 (3 (цм).

Ова формула се не мора памтити. Довољно је подсјетити да висина дијели трокут на два правокутна. Штавише, испоставило се да је то нога, а хипотенуза у њој је страна оригинала, друга нога је половина познате стране. Сада морате написати Питагорину теорему и извући формулу за висину.

Одговор: висина је 6 цм 3 цм.

№3. Даје се МКР - троугао, 90 степени у коме се прави угао К. Странице МР и КР су познате, оне су једнаке 30 и 15 цм, односно потребно је утврдити вредност угла Р.

Одлука. Ако направите цртеж, постаје јасно да је МР хипотенуза. И то је двоструко више од КР. Поново се морате позвати на својства. Један од њих је повезан са угловима. Из њега је јасно да је угао ЦМР једнак 30º. Тако ће жељени угао П бити једнак 60º. Ово следи из другог својства, које каже да би збир два акутна угла требало да буде 90º.

Одговор: П угао је 60º.

№4. Морате пронаћи све углове једнакокрачног троугла. О њему је познато да је спољашњи угао од угла у бази 110º.

Одлука. Пошто је дат само спољашњи угао, то треба користити. Формира се са унутрашњим кут отклопљен. Дакле, укупно ће дати 180º. То значи да ће угао у основи троугла бити једнак 70º. Пошто је једнакокрачан, други угао има исто значење. Остаје да се израчуна трећи угао. По особини која је заједничка свим троугловима, сума углова је 180º. Дакле, трећи је дефинисан као 180º - 70º - 70º = 40º.

Одговор: углови су 70º, 70º, 40º.

№5. Познато је да је у једнакокрачном троуглу угао који лежи наспрам базе 90º. На основу означене тачке. Сегмент који га повезује правим углом га дели у односу од 1 до 4. Морате знати све углове мањег троугла.

Одлука. Један од углова се може одмах идентификовати. Од правоугаони троугао и једнакокрачне, онда ће оне које леже у њеној бази бити на 45º, односно на 90º / 2.

Други од њих ће помоћи у проналажењу познатог у односу увјета. Пошто је једнак 1 до 4, онда се делови у које је подељен добија само 5. Дакле, да би се открио мањи угао троугла, потребно је 90º / 5 = 18º. Остаје да научимо треће. Да бисте то урадили, од 180º (збир свих углова троугла), одузмите 45º и 18º. Прорачуни су једноставни и испадају: 117º.

Одговор: 18º, 45º, 117º