Шта је гравитациона константа?
После проучавања физике у умовима ученика све врсте трајних и њихових вредности. Тема гравитације и механике није изузетак. Најчешће не могу да одговоре на питање колико је важна гравитациона константа. Али они ће увек недвосмислено одговорити да је она присутна у закону светске ширине.
Из историје гравитационе константе
Занимљиво је да у радовима Њутна нема такве величине. У физици се појавила много касније. Конкретније, то је било тек почетком деветнаестог века. Али то не значи да није. Научници га једноставно нису идентификовали и нису препознали његово тачно значење. Говорећи о значењу. Гравитатионал константно стално како је наведено децимал са великим бројем цифара после децималне тачке, испред којих је нула.
Управо зато што ова количина претпоставља тако малу вредност, ефекат силе гравитације је невидљив на малим телима. Управо због овог мултипликатора, сила привлачења се испостави да је занемарива.
Први пут је експериментално установио вредност коју је преузела гравитациона константа, физичар Г. Цавендисх. И то се догодило 1788. године.

У својим експериментима користио је танку шипку. Била је обешена на танку бакарну жицу и имала дужину од око 2 метра. На крајеве ове шипке причвршћене су двије идентичне оловне куглице промјера 5 цм, а поред њих су постављене велике оловне куглице. Њихов пречник је већ био 20 цм.
При приближавању великих и малих куглица, уочена је ротација штапа. Говорио је о њиховој привлачности. Из познатих маса и растојања, као и измерене силе увијања, било је могуће сасвим тачно сазнати која је гравитациона константа једнака.
Све је почело слободним падом тела.
Ако сместимо тела различите масе у празнину, онда ће пасти у исто време. Под условом да падну са исте висине и почну истовремено. Било је могуће израчунати убрзање са којим сва тела падају на Земљу. Показало се да је приближно једнако 9,8 м / с2.
Научници су открили да је сила са којом се све привлачи Земља увијек присутна. И то не зависи од висине на коју се тело креће. Један метар, километар или стотине километара. Без обзира колико је тело далеко, привући ће га Земља. Друго питање је како ће његова вриједност овисити о удаљености?
На то је питање одговорио енглески физичар И. Њутн.
Смањење силе привлачења тијела са њиховом удаљености
За почетак, сугерирао је да се сила гравитације смањује. Његова вредност је обрнуто повезана са квадратом удаљености. Штавише, ова удаљеност се мора рачунати од центра планете. И он је направио теоријске калкулације.
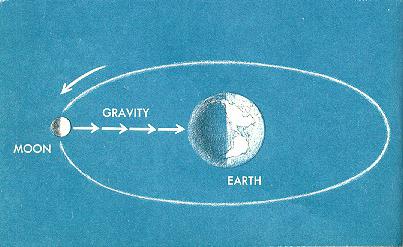
Тада је овај научник користио податке астронома о кретању природног сателита Земље - Месеца. Њутн је израчунао убрзање којим се окреће око планете и добио исте резултате. То је сведочило о истинитости његовог расуђивања и дозвољеном формулисању закон света. Гравитациона константа у његовој формули до сада није била присутна. У овој фази је било важно утврдити зависност. Шта је урађено. Гравитација се смањује обрнуто од квадрата на удаљености од центра планете.
Закону света
Њутн је наставио размишљати. Пошто Земља привлачи Месец, онда га и сама привлачи Сунце. Штавише, сила такве привлачности такође треба да поштује закон који је он описао. А онда га је Њутн проширио на сва тела универзума. Према томе, назив закона укључује ријеч "универзално".
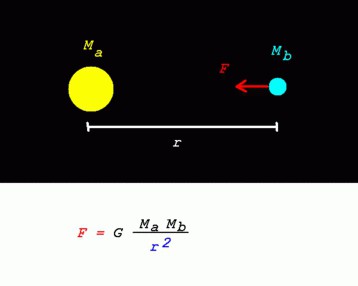
Снаге светских тела дефинисане су као пропорционално зависне од производа масе и обрнуто од квадрата удаљености. Касније, када је одређен коефицијент, формула закона је добила сљедећи облик:
- Ф т = Г (м к к м 2 ): р 2 .
Садржи следећу нотацију:
| Снага | Ф т |
| Гравитациона константа | Г |
| Боди масс | м 1 , м 2 |
| Удаљеност између тела | р |
Формула за гравитациону константу следи из овог закона:
- Г = (Фт Кс р 2 ): (м 1 к м 2 ).
Вредност гравитационе константе
Сада је дошао ред на одређене бројеве. Пошто научници стално појашњавају ову вредност, различити бројеви су званично усвојени у различитим годинама. На пример, према подацима за 2008. годину, гравитациона константа је 6.6742 к 10 -11 Нм 2 / кг 2 . Три године су прошле - и константа се броји. Сада је гравитациона константа 6,6738 к 10 -11 Нм 2 / кг 2 . Међутим, за ученике у рјешавању проблема, његово заокруживање на такву вриједност је прихватљиво: 6,67 к 10 -11 Нм 2 / кг 2 .
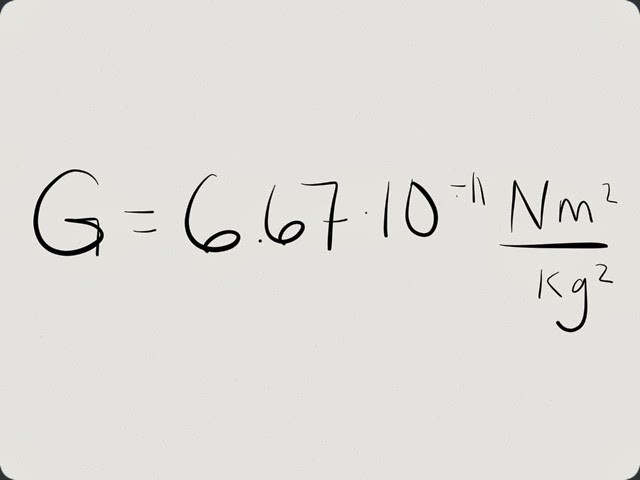
Који је физички смисао овог броја?
Ако у формули, која је дата за закон света, да замени конкретне бројеве, добијете занимљив резултат. У конкретном случају, када су масе тела једнаке 1 килограму, а налазе се на растојању од 1 метра, снага силе је једнака самом броју, који је познат по гравитационој константи.
Односно, значење гравитационе константе је то што показује с којом силом ће таква тела бити привучена на удаљености од једног метра. По броју можете видјети колико је та сила мала. На крају крајева, то је десет милијарди мање од једног. Немогуће је приметити. Чак и са повећањем тела сто пута, резултат се неће значајно променити. И даље остаје много мање од једног. Стога постаје јасно зашто је сила привлачења примјетна само у оним ситуацијама ако барем једно тијело има велику масу. На пример, планета или звезда.
Како је гравитациона константа са убрзањем слободан пад?
Ако упоредимо две формуле, од којих ће једна бити за гравитацију, а другу за закон Земље, можемо видети једноставан образац. Гравитациона константа, маса Земље и квадрат раздаљине од центра планете чине коефицијент који је једнак убрзајте слободан пад. Ако напишете ову формулу, добићете следеће:
- г = (Г к М): р 2 .
И користи следећу нотацију:
| Маса Земље | М |
| Радијус Земље | р |
Иначе, гравитацијска константа се може наћи из ове формуле:
- Г = (г к р 2 ): М.
Ако желите знати убрзање слободног пада на одређеној висини изнад површине планете, онда је ова формула корисна:
- г = (Г к М): (р + н) 2 , где је н висина изнад површине земље.
Задаци који захтевају знање о гравитационој константи
Први задатак
Цондитион Какво је убрзање слободног пада на једној од планета Сунчевог система, на пример, на Марсу? Познато је да је његова маса 6,23 · 10 23 кг, а радијус планете 3,38 · 10 6 м.
Одлука . Морате да користите формулу која је написана за Земљу. Само да замени вредности дате у задатку. Испоставља се да ће убрзање слободног пада бити једнако производу од 6,67 к 10 -11 и 6,23 к 10 23 , који се онда мора подијелити на квадрат од 3,38 · 10 6 . У бројнику се добија вредност од 41,55 к 10 12 . А именитељ ће бити 11.42 к 10 12 . Степени ће бити смањени, па је за одговор довољно знати само количник два броја.
Одговор : 3.64 м / с 2 .
Задатак два
Цондитион Шта треба урадити са телима како би смањили силу гравитације за 100 пута?
Одлука . Пошто се маса тела не може променити, сила ће се смањити због њиховог уклањања. Сто се добија из квадрирања 10. То значи да удаљеност између њих треба да буде 10 пута већа.
Одговор : удаљите их 10 пута од оригиналне удаљености.