Све опције о томе како пронаћи трапезоидну област
Многостран трапез ... Може бити произвољан, једнакокрачан или правокутан. И у сваком случају, морате знати како пронаћи подручје трапеза. Наравно, најлакши начин за памћење основних формула. Али понекад је лакше користити ону која је изведена са свим особинама одређеног геометријски облик.
Неколико речи о трапезу и његовим елементима
Било који четверокут чије су двије стране паралелне може се назвати трапез. У принципу, они нису једнаки и називају се основама. Већи од њих је нижи, а други је горњи.
Друге две стране су бочне. За произвољни трапез, они имају различите дужине. Ако су једнаки, онда та цифра постаје једнакокрачна.
Ако је изненада кут између било које стране и базе 90 степени, онда је трапез правокутан.
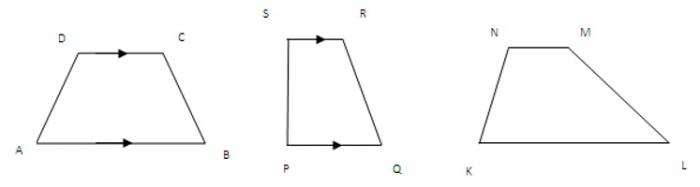
Све ове особине могу помоћи у рјешавању проблема како пронаћи подручје трапеза.
Међу елементима фигуре који могу бити неопходни у решавању проблема, можемо нагласити следеће:
- висина, тј. сегмент окомит на обје базе;
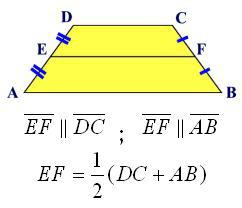
- средњу линију, која са својим крајевима има средњу страну.
По којој формули израчунати подручје, ако знате основицу и висину?
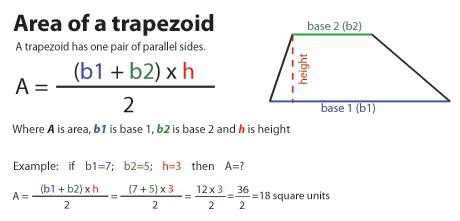
Овај израз даје главни, јер најчешће можете препознати те вредности, чак и када нису изричито дате. Дакле, да разумемо како да нађемо трапезно подручје мораћете да оборите обе базе и поделите их на два дела. Резултујућа вредност се тада множи са вредностима висине.
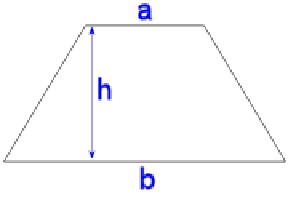
Ако основама означимо слова а 1 и а 2 , висина је н, онда ће формула за подручје изгледати овако:
С = ((а 1 + а 2 ) / 2) * н.
Формула за израчунавање површине, ако је дата њена висина и средња линија
Ако пажљиво погледате претходну формулу, лако је уочити да је вредност средње линије јасно присутна у њој. Наиме, збир база подељен са два. Нека средња линија буде означена словом л, а формула за подручје ће бити овако:
С = л * н.
Способност проналажења подручја дијагонално
Овај метод ће вам помоћи ако знате угао који они формирају. Претпоставимо да су дијагонале означене словима к 1 и г 2 , а углови између њих су α и β. Тада ће се формула како пронаћи подручје трапеза написати на следећи начин:
С = ((д 1 * д 2 ) / 2) * син α.
У овом изразу, лако можете заменити α са β. Резултат се неће променити.
Како сазнати подручје ако су све стране фигуре познате?
Постоје и ситуације када су тачно познате стране на овој слици. Ова формула је гломазна и тешка за памћење. Али је могуће. Нека стране имају ознаку: у 1 и 2 , базу и 1 више од 2 . Тада ће формула подручја изгледати овако:
С = ((а 1 + а 2 ) / 2) * √ {у 1 2 - [(а 1 - а 2 ) 2 + у 1 2 - у 2 2 ) / (2 * (а 1 - а 2 )) ] 2 }.
Начини за израчунавање површине једнакокрачног трапеза
Први се односи на чињеницу да се у њега може ући круг. И, знајући његов радијус (означен је словом р), као и угао на бази - γ, можете користити следећу формулу:
С = (4 * р 2 ) / син γ.
Ова друга општа формула, која се заснива на познавању свих страна слике, бит ће значајно поједностављена због чињенице да стране имају исто значење:
С = ((а 1 + а 2 ) / 2) * √ {у 2 - [(а 1 - а 2 ) 2 / (2 * (а 1 - а 2 ))] 2 }.
Методе за израчунавање површине правоугаоног трапеза
Јасно је да ће било који од набројаних за произвољан облик то урадити. Али понекад је корисно знати за једну особину таквог трапеза. Она лежи у чињеници да је разлика квадрата дужина дијагонала једнака разлици која се састоји од квадрата база.
Често се формуле за трапезоид заборављају, док се изрази за области правокутника и троугла памте. Онда можете применити једноставан начин. Поделите трапез у два облика, ако је правоугаон, или три. Један тачно ће бити правоугаоник, а други или два преостала троугла. Након израчунавања подручја ових цифара само ће их додати.
Ово је прилично једноставан начин како пронаћи квадрат трапез.
Шта ако су познате координате врхова трапеза?
У овом случају, мораћете да користите израз који вам омогућава да одредите растојање између тачака. Може се наносити три пута: како би се научиле обје базе и једна висина. И онда само примените прву формулу, која је описана мало више.
Да бисте илустровали овај метод, можете дати пример. Добијени врхови са координатама А (5; 7), Б (8; 7), Ц (10; 1), Д (1; 1). Потребно је знати подручје слике.
Пре него што пронађете подручје трапеза, потребно је да израчунате дужине базе помоћу координата. Требаће вам следећа формула:
дужина сегмента = √ {(разлика првих координата тачака) 2 + (разлика других координата тачака) 2 }.
Горња база је означена са АБ, што значи да ће њена дужина бити једнака √ {(8-5) 2 + (7-7) 2 } = =9 = 3. Нижа ће бити СД = √ {(10-1) 2 + (1-1 ) 2 } = =81 = 9.
Сада треба да држите висину од врха до базе. Нека његов почетак буде у тачки А. Крај сегмента ће бити на доњој бази у тачки са координатама (5; 1), нека буде тачка Н. Дужина сегмента АН ће бити једнака √ {(5-5) 2 + (7-1) 2 } = =36 = 6.
Остаје само да се добијене вредности замене формулом за трапезоидну област:
С = ((3 + 9) / 2) * 6 = 36.
Проблем се рјешава без јединица, јер координатна мрежа није специфицирана. Може бити милиметар или метар.
Примери задатака
№ 1. Цондитион. Познат угао између дијагонала произвољног трапеза, једнак је 30 степени. Мања дијагонала је 3 дм, а друга 2 пута већа. Потребно је израчунати површину трапеза.
Одлука. Прво морате знати дужину друге дијагонале, јер без тога не можете рачунати на одговор. Израчунајте га лако, 3 * 2 = 6 (дм).
Сада морате користити одговарајућу формулу за подручје:
С = ((3 * 6) / 2) * син 30º = 18/2 * ½ = 4.5 (дм 2 ). Проблем решен.
Одговор: површина трапеза је 4,5 дм 2 .
№ 2. Стање. У трапезу АВСД, базе су АД и БЦ сегменти. Тачка Е је средина стране СД. Из њега је извучена окомита на правац АБ, крај овог сегмента је означен словом Н. Познато је да су дужине АБ и ЕХ 5 и 4 цм, па је потребно израчунати површину трапеза.
Одлука. Прво морате направити цртеж. Будући да је вредност окомице мања од стране на коју се води, трапез ће бити благо испружен према горе. Дакле, ЕН ће бити унутар слике.
Да бисте јасно видели напредак задатка, мораћете да извршите додатну конструкцију. Наиме, нацртајте правац који ће бити паралелан са страном АБ. Точке пресека ове линије са АД - П, и са наставком Оружаних снага - Кс. Резултат је паралелограм. Штавише, његова површина је једнака жељеној. То је због чињенице да су троуглови који су испали са додатном конструкцијом једнаки. Ово следи из једнакости стране и два угла поред њега, један - вертикални, други - лежећи унакрсно.
Подручје паралелограма можете пронаћи по формули, која садржи производ стране и висину на којој је падао.
Тако је површина трапеза 5 * 4 = 20 цм2.
Одговор: С = 20 цм 2 .
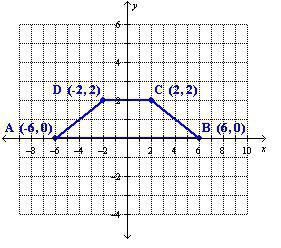
№ 3. Стање. Елементи једнакокрачног трапеза имају следећа значења: доња база је 14 цм, горња је 4 цм, а акутни угао 45º. Потребно је израчунати његову површину.
Одлука. Нека мања база буде означена као БЦ. Висина из тачке Б ће се звати ХВ. Пошто је угао 45º, троугао АБХ биће правоугаони и једнакокрачан. Дакле, АН = БХ. Штавише, НА је врло лако пронаћи. Она је једнака половини основне разлике. То је (14 - 4) / 2 = 10/2 = 5 (цм).
Основе су познате, висина се рачуна. Можете користити прву формулу, која је овде разматрана за произвољни трапезоид.
С = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (цм2).
Одговор: Потребна површина је 45 цм 2 .
№ 4. Стање. Постоји произвољни трапезоидни АВСД. На његовим странама, узимају се тачке О и Е, тако да је ОЕ паралелан са базом ковчега. Површина трапезног АОЕД-а је пет пута већа од површине ЦФЕ-а. Израчунајте ОЕ вредност ако су основне дужине познате.
Одлука. Потребно је нацртати двије паралелне АБ равне линије: прво кроз точку Ц, њено сјециште са ОЕ је точка Т; други кроз Е и тачку пресека са АД ће бити М.
Нека непозната ОЕ = к. Висина мањег трапеза ЦФЕ је н 1 ;
Будући да су подручја ова два трапеза повезана са 1 до 5, можемо написати следећу једнакост:
(к + а 2 ) * н 1 = 1/5 (к + а 1 ) * н 2
или
н 1 / н 2 = (к + а 1 ) / (5 (к + а 2 )).
Висине и стране троуглова су пропорционалне конструкцијом. Зато можемо да напишемо још једну једнакост:
н 1 / н 2 = (к - а 2 ) / (а 1 - к).
У последња два уноса на левој страни постоје једнаке вредности, тако да можете написати да је (к + а 1 ) / (5 (к + а 2 )) једнако (к - а 2 ) / (а 1 - к).
Ово захтева низ трансформација. Прво умножите унакрсно. Појављују се заграде које показују разлику у квадратима.Након примјене ове формуле добићете кратку једнаџбу.
Потребно је отворити заграде и помјерити све појмове из непознатог "к" на лијеву страну, а затим извадити скуаре роот.
Одговор : к = √ {(а 1 2 + 5 а 2 2 ) / 6}.