Како израчунати границе секвенци?
Математика је наука која гради свет. Као научник и једноставна особа - нико не може без тога. Прво, мала дјеца се уче рачунати, затим додавати, одузимати, умножавати и дијелити, у средњој школи се појављују ознаке, ау старијој не могу без њих.
Али данас ћемо говорити о томе на чему се гради сва позната математика. На заједници бројева који се називају "ограничења секвенци".
Шта су секвенце и где је њихова граница?
Значење ријечи "слијед" није тешко протумачити. То је конструкција ствари у којима је неко или нешто уређено у одређеном редоследу или реду. На пример, ред за улазнице у зоолошки врт - је редослед. И то може бити само један! Ако, на пример, погледате ред у продавници - ово је једна секвенца. И ако једна особа изненада напусти ову линију, онда је ово друга линија, други ред.
Реч "граница" се такође лако тумачи - то је крај нечега. Међутим, у математици, границе секвенци су оне вредности на линији бројева на које тежи низ бројева. Зашто тражи, а не завршава? Све је једноставно, бројчана линија нема краја, а већина секвенци, попут зрака, имају само почетак и изгледају овако:
к 1 , к 2 , к 3 , ... к н ...
Стога је дефиниција секвенце функција природног аргумента. Једноставније речено, то је низ чланова неког скупа.
Како је изграђен нумерички низ?
Најједноставнији пример нумеричког низа може изгледати овако: 1, 2, 3, 4, ... н ...
У већини случајева, за практичне сврхе, секвенце се граде из бројева, а сваки наредни члан серије, означен са Кс, има своје име. На пример:
к 1 - први члан секвенце;
к 2 - други члан секвенце;
к 3 - трећи члан;
...
к н је н- ти термин.
У практичним методама, редослед је дат општом формулом, у којој постоји нека променљива. На пример:
Кс н = 3н, онда ће сама серија бројева изгледати овако:
к 1 = 3;
к 2 = 6;
к 3 = 9;
и тако даље
Не треба заборавити да у општем запису секвенци можете користити било која латинична слова, не само Кс. На пример: и, з, к, итд.
Аритметичка прогресија као део секвенци
Пре него што потражимо границе секвенци, пожељно је дубље уронити у сам концепт таквог нумеричког низа, на који су се сви сусрели у средњој класи. Аритметичка прогресија је низ бројева у којима је разлика између сусједних чланова константна.
Задатак: “Нека је а 1 = 15, а корак прогресије нумеричке серије д = 4. Изградите првих 4 члана ове серије. "
Решење: а 1 = 15 (по стању) - први члан прогресије (серија бројева).
а 2 = 15 + 4 = 19 је други члан прогресије.
и 3 = 19 + 4 = 23 - трећи члан.
а 4 = 23 + 4 = 27 је четврти члан.
Међутим, овај метод је тешко постићи велике вредности, као што је 125 .. Посебно за такве случајеве, изведена је формула погодна за праксу: а н = а 1 + д (н - 1). У овом случају, а 125 = 15 + 4 (125-1) = 511.
Врсте секвенци
Већина секвенци је бескрајна, вреди памтити цео живот. Постоје два интересантна типа серија бројева. Прва је дата формулом а н = (- 1) н . Математичари ову секвенцу често називају бљеском. Зашто? Проверите његове нумеричке серије.
-1, 1, -1, 1, -1, 1, итд. Са таквим примером постаје јасно да се бројеви у секвенцама могу лако поновити.
Факторска секвенца. Лако је погодити - факторијал је присутан у формули која дефинише секвенцу. На пример: а н = (н + 1)!
Онда ће редослед изгледати овако:
а 1 = 1к2 = 2;
а 2 = 1к2к3 = 6;
а 3 = 1к2к3к4 = 24, итд.
Секвенца дефинисана аритметичком прогресијом назива се бескрајно опадајући ако се неједнакост -1 посматра за све њене чланове.
а 1 = - ½;
а 2 = ¼;
3 = - 1/8, итд.
Постоји чак и низ који се састоји од истог броја. Дакле, и н = 6 се састоји од бесконачног скупа шестица.
Одређивање границе секвенце
Границе секвенци већ дуго постоје у математици. Наравно, заслужили су свој компетентни дизајн. Дакле, време је да научите дефиницију граница секвенци. Прво, детаљно размотримо границу за линеарну функцију:
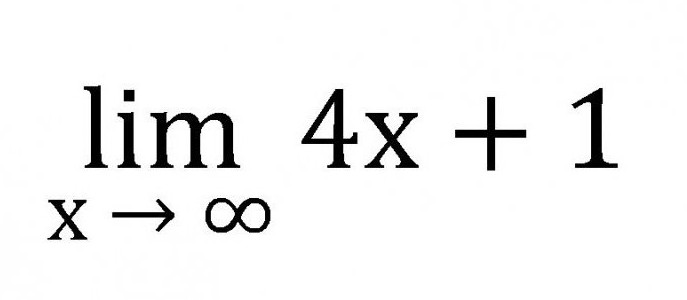
- Све границе су скраћене лим.
- Лимит запис се састоји од кратице лим, неке варијабле које теже до одређеног броја, нуле или бесконачности, као и из саме функције.
Лако је разумети да се дефиниција границе секвенце може формулисати на следећи начин: то је одређени број на који се сви чланови низа бесконачно приближавају. Једноставан пример: а к = 4к + 1. Онда ће сама секвенца изгледати овако.
5, 9, 13, 17, 21 ... к ...
Дакле, ова секвенца ће се бесконачно повећавати и, према томе, њена граница је једнака бесконачности као к → ∞, и то треба написати као:
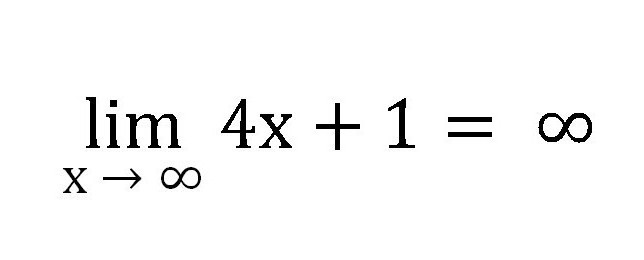
Ако узмемо сличан низ, али к ће тежити 1, добићемо:
а к = 4к + 1.
Низ бројева ће бити овако: 1.4, 1.8, 4.6, 4.944, и тако даље. Сваки пут морате да замените број све ближе једном (0.1, 0.2, 0.9, 0.986). Из ове серије је јасно да је граница функције пет.
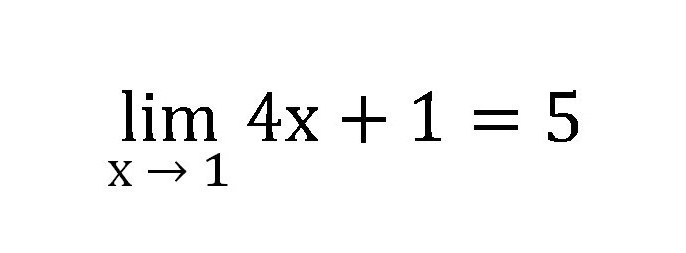
Из овог дијела треба запамтити границу нумеричког низа, дефиницију и метод рјешавања једноставних задатака.
Општа ознака границе секвенци
Испитујући границу нумеричког низа, његову дефиницију и примјере, можемо прећи на сложенију тему. Апсолутно све границе секвенци могу се формулисати са једном формулом, која се обично анализира у првом семестру.
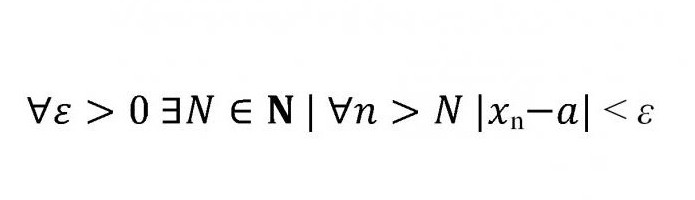
Шта значи овај скуп слова, модула и знакова неједнакости?
Куант - квантификатор универзалности, који замјењује изразе “за све”, “за све”, итд.
∃ - квантификатор постојања, у овом случају значи да постоји нека вриједност Н која припада скупу природни бројеви.
Дуги вертикални штап, пратећи Н, значи да је задати скуп Н "такав да." У пракси, то може значити "тако да", "тако да", итд.
Затим долази модул. Очигледно, модул је дистанца, која по дефиницији не може бити негативна. Дакле, модул модула је строго мањи од "епсилона".
Да би се материјал консолидовао, гласно прочитајте формулу.
Несигурност и одређеност ограничења
Метода проналажења границе секвенци, о којој смо већ говорили, је једноставна у употреби, али у пракси није толико рационална. Покушајте да пронађете границу за такву функцију:
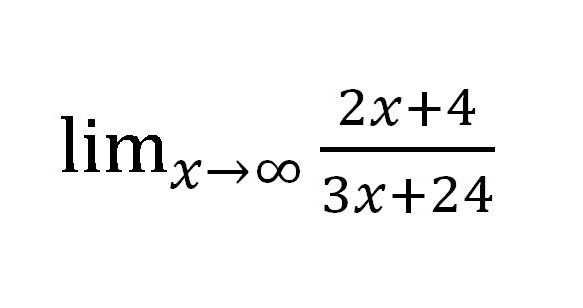
Ако заменимо различите вредности "Кс" (сваки пут се повећава: 10, 100, 1000, итд.), Онда у нумератору добијамо ∞, али у имениоцу такође ∞. Испада прилично чудна фракција: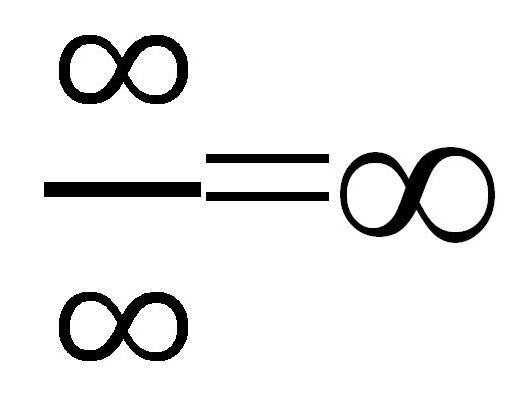 
Али је ли то стварно? Израчунајте границу нумеричког низа у овом случају изгледа прилично лако. Било би могуће оставити све како јесте, јер је одговор спреман, и примљен је под разумним условима, али постоји други начин посебно за такве случајеве.
За почетак, налазимо највећу снагу у нумератору фракције - она је 1, пошто к може бити представљена као к 1 .
Сада налазимо највећу моћ у имениоцу. Такође 1.
Поделимо и нумератор и именилац у варијаблу у највишем степену. У овом случају, фракција је дељива са к 1 .
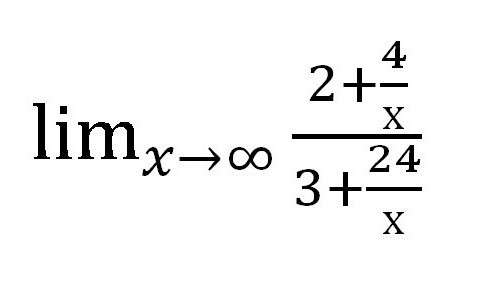
Затим ћемо пронаћи коју вредност ће сваки додатак који садржи променљиву тежити. У овом случају, фракција. Када је к → ∞, вредност сваке од фракција тежи нули. Приликом израде писаног рада, вреди направити такве фусноте:
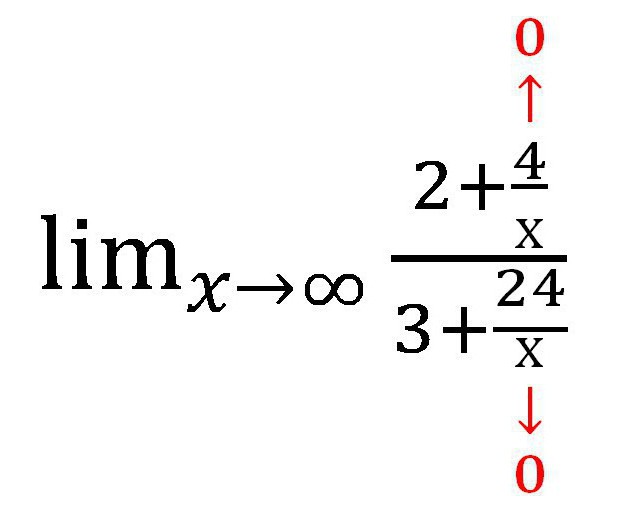
Добија се следећи израз:
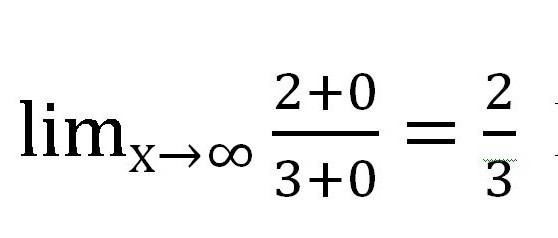
Наравно, фракције које садрже к нису постале нуле! Али њихова вредност је толико мала да је потпуно дозвољено да се не узме у обзир приликом израчунавања. У ствари, к никада неће бити једнако 0 у овом случају, јер се нула не може поделити.
Шта је комшилук?
Претпоставимо да професор има на располагању комплексну секвенцу, која се, очигледно, даје не мање комплексном формулом. Професор је нашао одговор, али да ли је прикладан? Уосталом, сви људи су у криву.
Аугусте Цауцхи је у своје време смислио одличан начин да докаже границе секвенци. Његов метод се звао операција суседства.
Претпоставимо да постоји нека тачка а, њено суседство у оба правца на бројној линији је ε ("епсилон"). Пошто је последња променљива дистанца, њена вредност је увек позитивна.
Сада дефинишемо неку секвенцу к н и претпоставимо да је десети члан секвенце (к 10 ) улази у сусједство а. Како написати ову чињеницу на математичком језику?
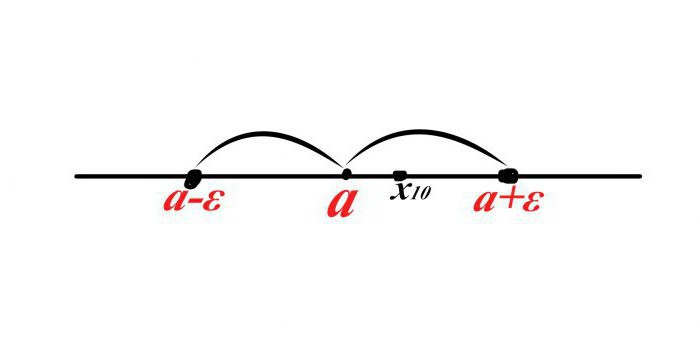
Претпоставимо да је к 10 десно од тачке а, онда је удаљеност к 10 –а <ε, међутим, ако поставите „Кс десети“ лево од тачке а, онда ће удаљеност бити негативна, али то је немогуће, онда треба да додате леву страну неједнакости на Добијамо | к 10 –а | <ε.
Сада је време да се у пракси појасни та формула која је горе поменута. Одређени број а се с правом назива крајња тачка секвенце ако је за било које од њених ограничења задовољена неједнакост ε> 0, а цело суседство има свој природни број Н, тако да ће сви чланови секвенце са значајнијим бројевима бити унутар секвенце | к н - а | <ε .
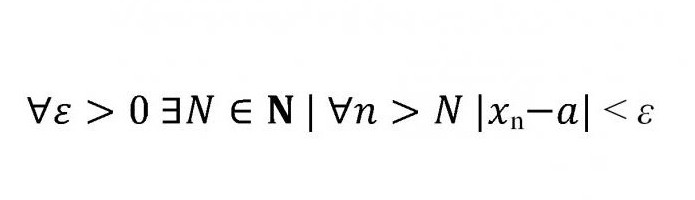
Са таквим знањем, лако је имплементирати рјешење до граница низа, доказати или оповргнути спреман одговор.
Теореми
Теореме ограничења секвенци су важна компонента теорије, без које је пракса немогућа. Постоје само четири главне теореме, које памте, а понекад је могуће олакшати ток решења или доказа:
- Јединственост границе секвенце. Граница за било коју секвенцу може бити само једна или не. Исти пример са редом, који може имати само један крај.
- Ако низ бројева има ограничење, онда је редослед ових бројева ограничен.
- Граница суме (разлика, производ) секвенци је једнака суми (разлика, производ) њихових граница.
- Граница квоцијента од подјеле двије секвенце једнака је количнику граница ако и само ако називник не нестаје.
Доказ о секвенцама
Понекад је потребно ријешити инверзни проблем, како би се доказала задана граница нумеричког низа. Размотрите пример.
Доказати да је граница секвенце коју даје формула једнака нули.
У складу са горе наведеним правилом, за било који редослед неједнакост | к н мора бити задовољена - а | <ε. Замените наведену вредност и референтну тачку. Добијамо:
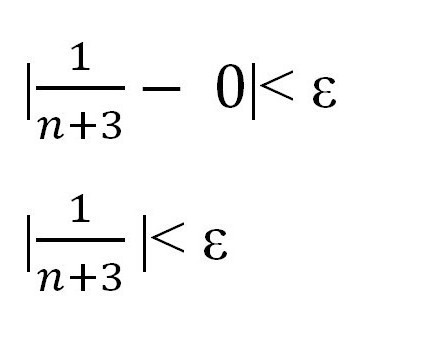
Изразите "кроз епсилон" да бисте показали постојање одређеног броја и доказали постојање граничног низа.
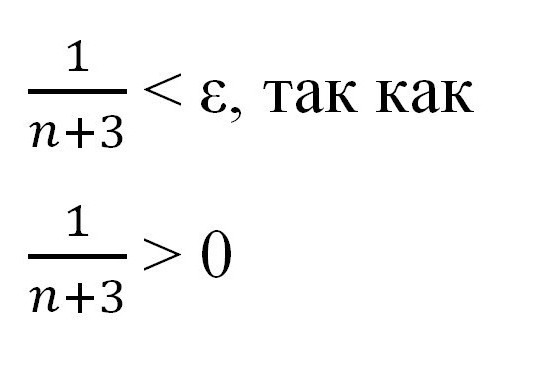
У овој фази, важно је подсјетити да су "епсилон" и "ен" бројеви позитивни и не-нула. Сада можете наставити даље трансформације користећи знање о неједнакостима које сте добили у средњој школи.
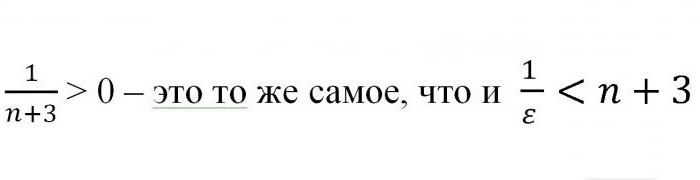
Одатле се испоставља да је н> –3 + 1 / ε. Пошто је вредно сетити се да говоримо о природним бројевима, резултат се може заокружити стављањем у углате заграде. Тако је доказано да је за сваку вредност суседног “епсилона” тацке а = 0 постојала таква вредност да поцетна неједнакост важи. Из овога можемо са сигурношћу рећи да је број а граница дате секвенце. Шта је било потребно да се докаже.
Са таквом погодном методом, може се доказати граница нумеричког низа, колико год да је на први поглед комплексан. Главна ствар - не паничарити при погледу на посао.
Или можда није?
Постојање ограничавајућег низа је опционално у пракси. Лако можете пронаћи такав низ бројева који заиста немају краја. На пример, исти фласхер к н = (–1) н . очигледно је да секвенца која се састоји од само два броја, циклично понављајућа, не може имати ограничење.
Иста историја се понавља са секвенцама које се састоје од једног броја, фракционисаног, имајући у току калкулација несигурност било ког поретка (0/0, ∞ / ∞, 0/0, итд.). Међутим, треба имати на уму да је дошло и до погрешног обрачуна. Понекад ће ограничење секвенци помоћи да поново проверите своја решења.
Монотоне секуенце
Изнад смо размотрили неколико примјера секвенци, методе за њихово рјешавање, а сада ћемо покушати узети још специфичнији случај и назвати га “монотоним слиједом”.
Дефиниција: поштено је назвати било коју секвенцу монотоно растућу ако за њу важи стриктна неједнакост к н <к н +1. Такође, свака секвенца се с правом назива монотонско опадање ако за њу важи неједнакост к н > к н +1.
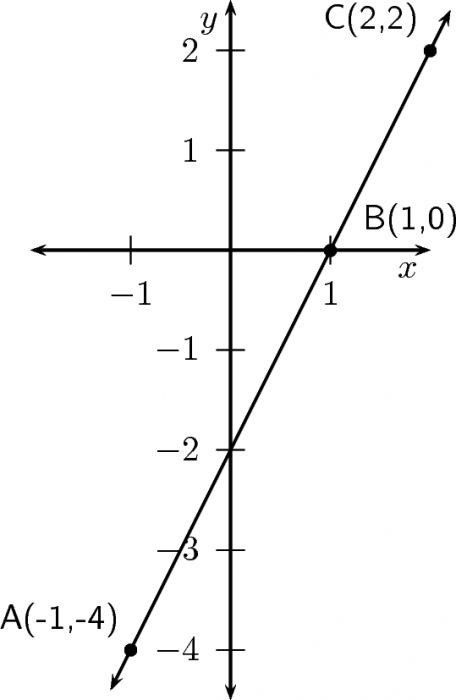
Уз ова два услова, постоје и сличне слабе неједнакости. Сходно томе, к н ≤ к н +1 (секвенца која се не смањује) и к н ≥ к н +1 (секвенца која се не повећава).
Али то је лакше разумети са примерима.
Секвенца коју даје формула к н = 2 + н формира следећу серију бројева: 4, 5, 6, итд. Ово је монотоно растућа секвенца.
А ако узмемо к н = 1 / н, добијамо серију: 1/3, ¼, 1/5, итд. Ово је монотоно опадајућа секвенца.
Граница конвергентног и ограниченог низа
Ограничена секвенца - секвенца која има ограничење. Конвергентна секвенца је низ бројева који имају бесконачно мало ограничење.
Према томе, граница ограничене секвенце је ваљана или комплексни број. Запамтите да постоји само једна граница.
Граница конвергентне секвенце је инфинитезимална количина (реална или комплексна). Ако нацртате дијаграм секвенце, онда ће се у одређеној тачки чинити да се приближава, тежи да се окрене на одређену вредност. Отуда име - конвергентна секвенца.
Монотоноус лимит
Ограничење за такав низ може или не мора бити. У почетку је корисно разумети када је то, од кога се може одгурнути када доказује одсуство ограничења.
Међу монотоним секвенцама емитује се конвергирање и дивергирање. Конвергирање је низ који се формира скупом к и има реално или комплексно ограничење у скупу. Дивергентна - секвенца која нема ограничења у свом скупу (нити реална нити комплексна).
Поред тога, секвенца се конвергира ако се њена геометријска слика конвергира у горњу и доњу границу.
Граница конвергентне секвенце у многим случајевима може бити једнака нули, јер свака бесконачно мала секвенца има познато ограничење (нула).
Без обзира на конвергентну секвенцу, све су оне ограничене, али не све ограничене секвенце конвергирају.
Сума, разлика, производ двају конвергентних секвенци је такође конвергентна секвенца. Међутим, квоцијент може бити и конвергентан ако је дефинисан!
Разне акције са ограничењима
Границе секвенци су једнако значајне (у већини случајева) као бројеви и бројеви: 1, 2, 15, 24, 362, итд. Испоставило се да се неке операције могу обавити са ограничењима.
Прво, као и бројеви и бројеви, границе било које секвенце се могу додати и одузети. На основу треће теореме о границама секвенци, следи следећа једнакост: граница сума секвенци је једнака суми њихових граница.
Друго, на основу четврте теореме о границама секвенци, следећа једнакост је истинита: граница производа н-тог броја секвенци је једнака производу њихових граница. Исто важи и за поделу: граница квоцијента две секвенце је једнака количнику њихових граница, под условом да граница није нула. На крају крајева, ако је граница секвенци једнака нули, онда добијамо подела на нулу, што је немогуће.
Својства секвенци
Чини се да је граница нумеричког низа већ детаљно анализирана, али се такви изрази као што су „бесконачно мали“ и „бесконачно велики“ бројеви спомињу више пута. Очигледно, ако постоји секвенца 1 / к, где је к → ∞, онда је таква фракција бесконачно мала, и ако је секвенца иста, али граница тежи нули (к → 0), тада фракција постаје бесконачно велика количина. Такве количине имају своје карактеристике. Својства границе секвенце која има било које мале или велике вредности су следеће:
- Збир било које количине произвољно малих количина такође ће бити мала количина.
- Збир било ког броја великих количина биће бесконачно велика количина.
- Производ произвољно малих количина је бесконачно мали.
- Производ било ког броја великих бројева је бесконачно велика вредност.
- Ако оригинална секвенца тежи ка бесконачно великом броју, тада ће количина која је супротна њој бити бесконачно мала и тежи нули.
У ствари, израчунавање лимита низа није тако тежак задатак ако знате једноставан алгоритам. Али границе секвенци - тема која захтева максималну пажњу и истрајност. Наравно, довољно је само ухватити суштину решења таквих израза. Почевши од малог, временом можете доћи до великих врхова.