Регресиона једначина Једнаџба вишеструке регресије

Током студија ученици се често сусрећу са различитим једнаџбама. Један од њих - регресиона једначина - разматра се у овом чланку. Овај тип једначине се користи специфично за описивање карактеристика односа између математичких параметара. Овај тип једнакости се користи у статистици и економетрији.

Дефиниција регресије

У математици, регресија се односи на одређену вриједност која описује зависност просјечне вриједности укупности података од вриједности друге вриједности. Регресиона једначина показује просечну вредност другог атрибута као функцију одређеног атрибута. Регресиона функција има облик једноставне једначине и = к, у којој је и зависна варијабла, а к је независна (сигн-фацтор). У ствари, регресија је изражена као и = ф (к).

Које су врсте односа између варијабли?

Генерално, два супротна типа интерконекције истичу се: корелација и регресија.

Први карактерише једнакост условних варијабли. У овом случају, није поуздано познато која варијабла зависи од друге.

Ако не постоји једнакост између варијабли и у условима се каже која варијабла објашњава и која је зависна, онда можемо говорити о присутности другог типа везе. Да би се конструисала једнаџба линеарне регресије, неопходно је утврдити који тип односа се посматра.

Врсте регресија

До данас постоји 7 различитих типова регресије: хиперболички, линеарни, вишеструки, нелинеарни, парни, инверзни, логаритамски линеарни.

Хиперболична, линеарна и логаритамска

Линеар екуатион Регресије се користе у статистици да би се јасно објаснили параметри једначине. Изгледа да је и = ц + т * к + е. Хиперболичка једначина има облик регуларне хиперболе: и = ц + т / к + Е. Логаритмично линеарна једначина изражава однос користећи логаритамску функцију: У и = Ин ц + т * Ин к + Ин Е.

Множина и нелинеарност

Два сложенија типа регресије су вишеструка и нелинеарна. Једначина вишеструке регресије изражена је функцијом и = ф (к ₁ , к ₂ ... к _ц ) + Е. У овој ситуацији, и је зависна варијабла, а к је експланаторна варијабла. Варијабла Е је стохастичка, она укључује утицај других фактора у једначини. Једначина нелинеарне регресије је помало контрадикторна. С једне стране, с обзиром на узете у обзир индикаторе, он није линеаран, али с друге стране, у улози евалуације индикатора, он је линеаран.

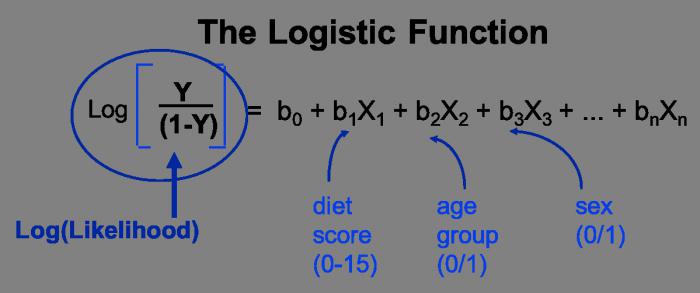
Обрнути и упарени типови регресија

Инверзна је врста функције која се мора претворити у линеарни облик. У најтрадиционалнијим апликативним програмима, он има облик функције и = 1 / с + т * к + Е. Једначина парова регресије показује однос између података као функције и = ф (к) + Е. Као и код других једначина, и зависи од к, а Е је стохастички параметар.

Концепт корелације

Ово је показатељ који показује постојање односа између два феномена или процеса. Снага односа се изражава као коефицијент корелације. Његова вредност флуктуира унутар интервала [-1; +1]. Негативан индикатор указује на присутност повратне информације, а позитивна на директну. Ако коефицијент има вредност 0, онда нема везе. Што је вриједност ближа 1, јача је веза између параметара, што је ближа 0, то је слабија.

Метходс

Корелационе параметарске методе могу да процене блискост односа. Они се користе на основу процјене дистрибуције за проучавање параметара који поштују закон нормалне дистрибуције.

Параметри једначине линеарне регресије су потребни да би се идентификовао тип зависности, функција регресионе једначине и процена индикатора изабране формуле за међусобну повезаност. Поље корелације се користи као метода идентификације комуникације. Да бисте то урадили, сви постојећи подаци морају бити приказани графички. У правокутном дводимензионалном координатном систему потребно је примијенити све познате податке. Ово формира поље корелације. Вредност описног фактора је обележена дуж осе апсцисе, док су вредности зависног фактора обележене дуж оси ординате. Ако постоји функционална веза између параметара, они су распоређени у облику линије.

Ако је коефицијент корелације таквих података мањи од 30%, може се говорити о готово потпуном одсуству комуникације. Ако је између 30% и 70%, то указује на присуство карика средње чврстоће. 100% индикатор - доказ функционалне комуникације.

Једначина нелинеарне регресије, као и линеарна, мора бити допуњена корелационим индексом (Р).

Корелација вишеструке регресије

Коефицијент детерминације је индикатор квадрата вишеструке корелације. Говори о блискости односа приказаног скупа индикатора са испитиваном особином. Он такође може говорити о природи утицаја параметара на резултат. Једначина вишеструке регресије се процењује коришћењем овог индикатора.

Да би се израчунао индекс вишеструке корелације, потребно је израчунати његов индекс.

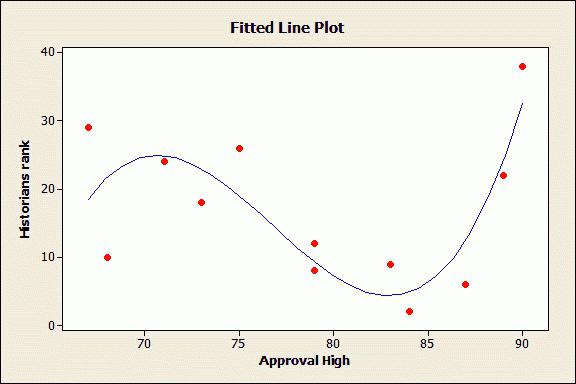
Метода најмањих квадрата

Овај метод је метода за процену фактора регресије. Његова суштина лежи у минимизирању суме одступања квадрата, добијеног због зависности фактора од функције.

Једнаџба линеарне регресије у пару може се проценити коришћењем ове методе. Овај тип једначина се користи у случају детекције између показатеља парног линеарног односа.

Параметри једначина

Сваки параметар функције линеарне регресије има специфично значење. Једначина упарене линеарне регресије садржи два параметра: с и м. Параметар т показује просечну промену у финалном индикатору функције и, подложно смањењу (повећању) варијабле к за једну конвенционалну јединицу. Ако је варијабла к нула, онда је функција једнака параметру ц. Ако варијабла к није нула, онда фактор ц нема економски смисао. Једини утицај на функцију има знак испред фактора ц. Ако постоји минус, онда можемо рећи о спорој промени резултата у односу на фактор. Ако постоји плус, онда то указује на убрзану промену резултата.

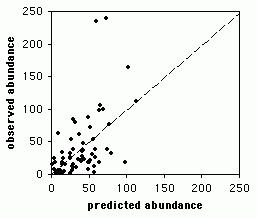
Сваки параметар који мења вредност регресионе једначине може се изразити преко једначине. На пример, фактор ц има облик ц = и - мк.

Груписани подаци

Постоје такви услови проблема у којима су све информације груписане на основу к, али истовремено за одређену групу су назначене одговарајуће средње вредности зависног индикатора. У овом случају, просечне вредности описују како се индекс, у зависности од к, мења. Дакле, групиране информације помажу у проналажењу једнаџбе регресије. Користи се као анализа односа. Међутим, овај метод има своје недостатке. Нажалост, просечни показатељи су често предмет спољних флуктуација. Ове осцилације нису одраз обрасца односа, оне само маскирају „буку“. Просеци показују да су обрасци односа много гори од линеарне регресионе једначине. Међутим, они се могу користити као основа за проналажење једначине. Помножавајући снагу једне популације са одговарајућим просеком, можете добити количину и унутар групе. Затим морате да поравнате све примљене износе и пронађете коначни индикатор. Мало теже направити калкулације са сумом ки. У том случају, ако су интервали мали, можете условно узети индикатор к за све јединице (унутар групе) исти. Потребно га је помножити са сумом и, како би се израчунао збир производа к по и. Даље, све количине се додају заједно и добије се укупна количина ки.

Вишеструка парна регресиона једначина: процена важности комуникације

Као што је раније дискутовано, вишеструка регресија има функцију облика и = ф (к ₁ , к ₂ , ..., к _м ) + Е. Најчешће се таква једначина користи за решавање проблема понуде и тражње за неким производом, доходак од камата на откупљене акције, за проучавање узрока и врсте функције трошкова производње. Такође се активно користи у широком спектру макроекономских студија и калкулација, али на микроекономском нивоу, таква једначина се користи мало мање.

Главни задатак вишеструке регресије је изградња модела података који садржи огроман количина информација како би се даље одредио утицај сваког од фактора одвојено и на њихову укупност на индикатор који ће се моделирати и његове коефицијенте. Регресиона једначина може имати широк спектар вредности. У исто време, за процену интерконекције најчешће се користе две врсте функција: линеарно и нелинеарно.

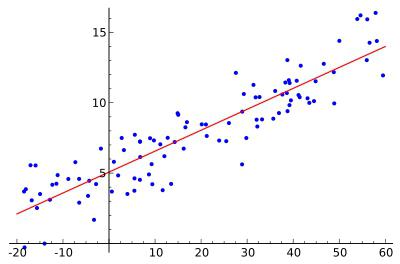
Линеарна функција је приказана у облику сљедеће везе: и = а ₀ + а ₁ к ₁ + а ₂ к ₂ , + ... + а _м к _м . У исто време, _а2, а _м , сматрају се “чистим” коефицијентима регресије. Они су неопходни за карактеризацију просечне промене параметра и са променом (смањењем или повећањем) у сваком одговарајућем параметру к за једну јединицу, уз услов стабилне вредности других индикатора.

Нелинеарне једначине, на пример, имају облик функције снаге и = ак ₁ ^б1 к ₂ ^б2 ... к _м ^бм . У овом случају, називају се индикатори б ₁ , б ₂ ..... б _м - коефицијенти еластичности они показују како се резултат мења (колико у%) са повећањем (смањењем) одговарајућег индикатора к за 1% и са стабилним индикатором преосталих фактора.

Који фактори треба узети у обзир приликом изградње вишеструке регресије

Да би се исправно конструисала вишеструка регресија, потребно је утврдити који фактори треба посветити посебну пажњу.

Неопходно је имати одређено разумијевање природе односа економских фактора и моделираног. Фактори који треба да буду укључени морају да одговоре на следеће критеријуме:

• Треба да буде предмет квантификације. Да би се користио фактор који описује квалитет објекта, у сваком случају, треба му дати квантитативни облик.
• Не би требало да постоји међусобна повезаност фактора или функционални однос. Такве акције најчешће доводе до неповратних посљедица - систем обичних једнаџби постаје безувјетан, а то подразумијева његову непоузданост и неодређеност процјена.
• У случају постојања великог корелационог индикатора, не постоји начин да се одреди изоловани утицај фактора на коначни резултат индикатора, па коефицијенти постају неинтерпретирани.

Методе изградње

Постоји велики број метода и метода који објашњавају како одабрати факторе за једнаџбу. Међутим, све ове методе се заснивају на избору коефицијената користећи индекс корелације. Међу њима су:

• Метод елиминације.
• Метода укључивања.
• Степ-би-степ регресијска анализа.

Прва метода укључује елиминацију свих коефицијената из кумулативног скупа. Други метод укључује увођење многих додатних фактора. Трећи је елиминација фактора који су раније коришћени за једначину. Свака од ових метода има право да постоји. Они имају своје предности и мане, али могу решити питање елиминисања непотребних индикатора на свој начин. По правилу, резултати добијени сваком појединачном методом су прилично блиски.

Методе мултиваријационе анализе

Такве методе за одређивање фактора заснивају се на разматрању појединачних комбинација међусобно повезаних особина. Они укључују дискриминантну анализу, препознавање лица, начин на који су главне компоненте и кластер анализа. Поред тога, ту је и факторска анализа међутим, појавио се због развоја компоненте методе. Све се користе у одређеним околностима, под одређеним условима и факторима.