Трапезоидна област: формуле и методе прорачуна

Да би се поуздано и успјешно ријешили проблеми у сатовима геометрије, није довољно научити формуле. Они прво морају разумети. Бојати се, а још више мрзити формуле, је непродуктивно. У овом чланку, расположиви језик ће анализирати различите начине за проналажење подручја трапеза. За боље овладавање релевантним правилима и теоремима, посветићемо одређену пажњу његовим особинама. Ово ће вам помоћи да разумете како правила функционишу иу којим случајевима треба применити ове или оне формуле.

Одредите трапезоид

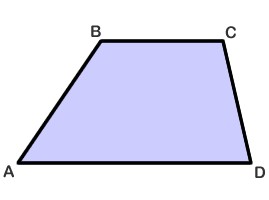Каква је та бројка уопште? Трапез је полигон са четири угла са две паралелне стране. Друге две стране трапеза могу бити нагнуте под различитим угловима. Његове паралелне стране називају се базама, а за непаралелне стране се користи назив "стране" или "кукови". Такве бројке су уобичајене у свакодневном животу. Контуре трапеза могу се видети у силуетама одеће, ентеријера, намештаја, посуђа и многих других. Трапез може бити различитих типова: свестран, једнакостран и правокутан. Више детаља о њиховим врстама и својствима биће објашњено касније у чланку.

Трапезоидна својства

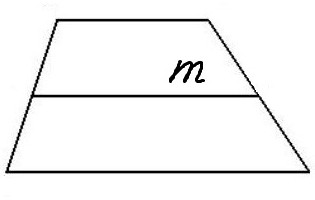Укратко ћемо расправити о својствима ове фигуре. Збир углова који се налазе на обе стране је увек 180 °. Треба напоменути да сви углови трапеза износе 360 °. Трапезиум има концепт средње линије. Ако повежете средине страна са сегментом, то ће бити средња линија. Означен је м. Средња линија има важна својства: она је увек паралелна са базама (памтимо да су базе такође паралелне једна са другом) и једнаке њиховој половини:

м = (а + б) / 2.

Ова дефиниција се мора научити и разумјети, јер је то кључ за рјешавање мноштва проблема!

У трапезу, висину увек можете спустити на базу. Висина је окомита, често означена симболом х, који се извлачи из било које тачке једне базе у другу базу или њен наставак. Средња линија и висина ће вам помоћи да пронађете подручје трапеза. Такви задаци су најчешћи у школској геометрији и редовно се појављују међу испитним и испитним радовима.

Најједноставније формуле трапезног подручја

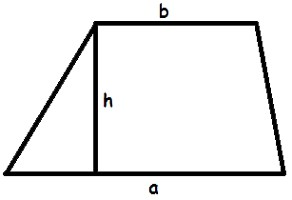Размотримо двије најпопуларније и једноставне формуле помоћу којих можемо пронаћи подручје трапеза. Довољно је да висину помножите са пола сума база да бисте лако пронашли жељени:

С = х * (а + б) / 2.

У овој формули, а, б означавају базу трапеза, х - висину. Ради лакшег опажања, у овом чланку знакови множења су означени симболом (*) у формулама, иако је у званичним референтним књигама знак множења обично изостављен.

Размотрите пример.

С обзиром на трапезоид са две базе од 10 и 14 цм, висина је 7 цм. Која је површина трапеза?

Хајде да анализирамо решење овог проблема. Према овој формули, прво треба да нађете полу-суму база: (10 + 14) / 2 = 12. Дакле, полу-сума је 12 цм, а сада помножимо полу суму по висини: 12 * 7 = 84. Потребно је наћи. Одговор: површина трапеза је 84 квадратна метра. види

Друга позната формула каже: површина трапеза је једнака производу средишње линије и висини трапеза. То је, у ствари, из претходног концепта средње линије: С = м * х.

Коришћење дијагонала за прорачуне

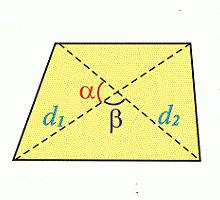
Други начин проналажења трапезоидног подручја заправо није толико компликован. Повезан је са његовим дијагоналама. Према овој формули, да би се пронашла област, потребно је да се полупроизвод његових дијагонала (д ₁ д ₂ ) помножи синусом угла између њих:

С = ½ д ₁ д ₂ син а.

Размотрите задатак који показује примену ове методе. С обзиром на: трапезоид са дужином дијагонала 8 и 13 цм, угао а између дијагонала је 30 °. Нађите подручје трапеза.

Одлука. Користећи горњу формулу, лако је израчунати потребну. Као што знате, грех 30 ° је 0.5. Дакле, С = 8 * 13 * 0.5 = 52. Одговор: површина је 52 квадратна метра. види

Тражимо подручје једнакостраничног трапеза.

Трапез може бити једнакостран (једнакокрачан). Њене стране су исте, а углови у подножју су једнаки, што добро илуструје цртеж. Једнакостранична трапеза има исте особине као и редовна, плус одређени број посебних. Круг се може описати око екиполарног трапеза, ау њега се може уписати круг.

Које су методе израчунавања површине такве фигуре? Следећи метод захтева велике израчуне. Да бисте га користили, морате знати вредности синуса (син) и косинуса (цос) угла на бази трапеза. Да бисте их израчунали, потребне су Брадис табеле или инжењерски калкулатор. Ево ове формуле:

С = ц * син а * ( а - ц * цос а ),

где је ц бочна бутина, а је угао на доњој бази.

Једнакостранична трапеза има дијагонале исте дужине. Обрнуто је исто: ако је дијагонална трапеза једнака, онда је то једнакост. Стога је следећа формула која помаже да се нађе површина трапеза полупроизвод квадрата дијагонала на синусу угла између њих: С = ½ д ² син а.

Нађите подручје правоугаоног трапеза

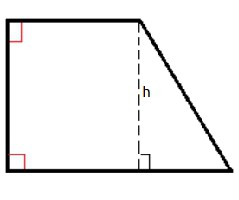
Познати специјални случај рецтангулар трапезоид. Ово је трапезоид, у коме је једна страна (бутина) суседна базама под правим углом. Има својства обичног трапеза. Поред тога, има веома интересантну особину. Разлика квадрата дијагонала таквог трапеза једнака је разлици квадрата њених база. За то користе све претходно описане методе за израчунавање површине.

Аппли ингенуити

Постоји један трик који може помоћи у случају заборављивости специфичних формула. Пажљиво размотрите шта је трапез. Ако га ментално поделимо на делове, постајемо познати и разумљиви геометријски облици: квадрат или правоугаоник и троугао (један или два). Ако су висина и стране трапеза познате, можете користити формуле троугао и правоугаоник, затим саберите све добијене вредности.

Ово илуструјемо следећим примером. Дати правокутни трапезоид. Угао Ц = 45 °, углови А, Д су 90 °. Горња база трапеза је 20 цм, висина 16 цм, а потребно је израчунати површину фигуре.

Решење

Ова бројка се очигледно састоји од правоугаоника (ако су два угла 90 °) и троугла. Будући да је трапез правоугаоник, његова висина је једнака његовој страни, тј. 16 цм, а имамо правоугаоник са странама од 20 и 16 цм. Размотримо сада троугао чији је угао 45 °. Знамо да је једна страна 16 цм, јер је та страна истовремено висина трапеза (и знамо да висина пада под базу под правим углом), тако да је други угао троугла 90 °. Стога је преостали угао троугла 45 °. Посљедица тога је да добијамо правокутни једнакокрачан трокут, чије двије стране су исте. То значи да је друга страна троугла једнака висини, односно 16 цм, али остаје да се израчуна површина троугла и правоугаоника и додају добијене вредности.

Ареа правоугаони троугао једнака половини производа његових ногу: С = (16 * 16) / 2 = 128. Површина правоугаоника једнака је продукту његове ширине по дужини: С = 20 * 16 = 320. Пронашли смо тражену: површину трапеза С = 128 + 320 = 448 квадрат. Можете једноставно поново да проверите да ли користите горе наведене формуле, а одговор ће бити идентичан.

Користите Пицк формулу

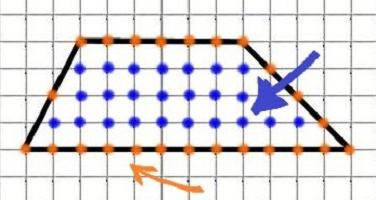
На крају, представљамо још једну оригиналну формулу која помаже да се пронађе подручје трапеза. Зове се Пицкова формула. Погодно је да се користи када је трапез нацртан на карираном папиру. Слични задаци се често налазе у ГИА материјалима. Изгледа овако:

С = М / 2 + Н - 1,

у овој формули, М је број чворова, тј. пресек линија слике са линијама ћелије на границама трапеза (наранџасте тачке на слици), Н је број чворова унутар фигуре (плаве тачке). Најпогодније је користити га за проналажење подручја неправилног полигона. Међутим, што је већи број коришћених метода, мање грешака и бољи резултати.

Наравно, дате информације су далеко од исцрпљености по врстама и својствима трапеза, као и методама трагања за његовим подручјем. Овај чланак даје преглед најважнијих карактеристика. Приликом решавања геометријских проблема, важно је поступати постепено, почети са једноставним формулама и задацима, конзистентно консолидовати разумевање, прећи на други ниво сложености.

Састављање најчешћих формула помоћи ће студентима да се оријентишу на различите начине како би израчунали површину трапеза и боље се припремили за тестове и тестове на ову тему.