Турингова машина: опис и примери Турингових машина
Турингова машина је једна од најинтригантнијих и најинтригантнијих интелектуалних открића 20. века. Ради се о једноставном и корисном апстрактном моделу рачунарства (компјутера и дигиталног), који је сасвим уобичајен за реализацију било којег компјутерског задатка. Захваљујући једноставном опису и понашању математичка анализа она чини темељ теоријске информатике. Ова студија је довела до дубљег знања о дигиталним рачунарима и рачуници, укључујући и разумевање да постоје неки рачунски проблеми који се не могу решити на уобичајеним корисничким рачунарима. 
Шта је то и ко је створио
Алан Туринг је покушао да опише нај примитивнији модел механичког уређаја који би имао исте основне могућности као и рачунар. Туринг је први пут описао аутомобил 1936. године у чланку "О израчунатим бројевима са применом на проблем решивости", који се појавио у Зборнику радова Лондонског математичког друштва. 
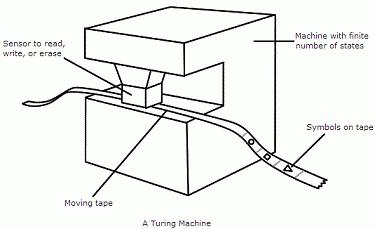
Турингова машина је рачунарски уређај који се састоји од главе за читање / писање (или "скенера") са папирном траком која пролази кроз њу. Трака је подељена на квадрате, од којих свака носи један знак - "0" или "1". Сврха механизма је да дјелује и као средство за улазак и излазак, и као радна меморија за похрањивање резултата средњих фаза прорачуна.
Од чега се уређај састоји
Свака таква машина се састоји од две компоненте:
- Неограничена трака. Бесконачно је у оба смера и подељено у ћелије.
- Аутоматски контролисан програм, скенер главе за читање и писање података. Може бити у сваком тренутку у једној од многих држава.
Свака машина повезује две коначне серије података: абецеду улазних симбола А = {а0, а1, ..., ам} и абецеду стања К = {к0, к1, ..., кп}. Стање к0 се назива пасивно. Верује се да уређај завршава свој рад када падне на њега. Стање к1 назива се иницијално - машина почиње своје калкулације, будући да је на почетку у њему. Улазна реч се налази на траци једног слова у реду у свакој позицији. На обе стране су само празне ћелије.
Како механизам функционише
Турингова машина има фундаменталну разлику у односу на рачунарске уређаје - њен меморијски уређај има бесконачну траку, док за дигиталне уређаје овај уређај има траку одређене дужине. Сваку класу задатака рјешава само једна изграђена Турингова машина. Други типови задатака укључују писање новог алгоритма.
Управљачки уређај, који је у једном стању, може се кретати у било којем смјеру дуж појаса. Он пише ћелијама и чита од њих знакове коначне абецеде. У процесу кретања, изабран је празан елемент који попуњава позиције које не садрже улазне податке. Алгоритам за Турингову машину одређује прелазна правила за контролни уређај. Они постављају главу за читање и писање на следеће параметре: уписивање у ћелију новог карактера, пребацивање у ново стање, померање лево или десно дуж траке. 
Својства механизма
Турингова машина, као и други рачунарски системи, има своја својствена својства и слична су својствима алгоритама:
- Дискретност Дигитална машина прелази на следећи корак н + 1 тек након што је претходни завршен. Сваки завршени корак додељује шта ће бити н + 1.
- Разумљивост Уређај обавља само једну радњу за исту ћелију. Убацује знак из абецеде и прави један покрет: лево или десно.
- Детерминизам. Свака позиција у механизму одговара појединачној реализацији специфициране шеме, а на свакој фази акције и редоследу њиховог извођења су недвосмислени.
- Перформансе. Тачан резултат за сваку фазу одређује Турингова машина. Програм извршава алгоритам иу коначном броју корака улази у стање к0.
- Масс. Сваки уређај је дефинисан изнад важећих ријечи у абецеди.
Турингове функције машине
Рјешење алгоритама често захтијева имплементацију функције. У зависности од могућности писања ланца за рачунање, функција се назива алгоритамски решивом или нерјешивом. Као скуп природних или рационалних бројева, речи у коначној абецеди Н за машину, разматра се секвенца скупа Б - речи унутар бинарне кодне абецеде Б = {0.1}. Резултат израчуна такође узима у обзир "недефинирану" вредност која се јавља када алгоритам виси. За имплементацију функције, важно је имати формални језик у коначној абецеди и рјешивост проблема препознавања исправних описа. 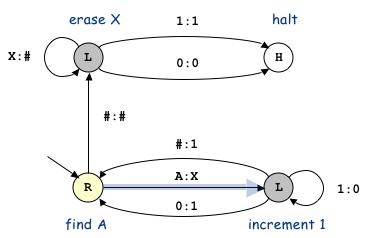
Програм за уређај
Програми за Турингов механизам формирани су табелама у којима први ред и колона садрже знакове вањске абецеде и вриједности могућих унутарњих стања аутомата - унутарње абецеде. Табеларни подаци су команде које Турингова машина опажа. Решавање проблема се дешава на овај начин: слово које чита глава у ћелији у којој се тренутно налази и унутрашње стање главе аутомата одређују која наредба треба да се изврши. Конкретно, таква команда се налази на пресеку симбола спољне абецеде и унутрашњег, који су у табели. 
Компоненте за прорачуне
Да би се направила Турингова машина за решавање једног специфичног задатка, потребно је одредити следеће параметре за њу.
Оутер алпхабет. Ово је неки коначни скуп симбола, означен знаком А, чији су саставни елементи названи слова. Један од њих - а0 - мора бити празан. На пример, абецеда Туринговог уређаја који ради са бинарним бројевима изгледа овако: А = {0, 1, а0}.
Континуирани низ алфанумеричких знакова записаних на траку се назива ријеч.
Аутоматска машина је уређај који ради без људске интервенције. У Туринговој машини, она има неколико различитих стања за решавање проблема и, под одређеним условима, креће се из једне позиције у другу. Комбинација таквих стања вагона је интерна абецеда. Има ознаку слова облика К = {к1, к2 ...}. Једна од ових одредби - к1 - треба да буде почетна, односно, шта покреће програм. Још један неопходан елемент је стање к0, које је коначно, то јест, довршава програм и ставља уређај у стоп позицију.
Табела конверзије. Ова компонента је алгоритам за понашање носача уређаја, у зависности од тренутног стања машине и вредности симбола који се чита. 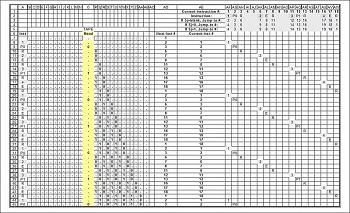
Алгоритам за аутомат
Превоз Туринговог уређаја у току рада контролише програм, који током сваког корака извршава редослед следећих акција:
- Писање спољашњег алфабетског знака на позицију, укључујући и празно, заменом елемента који је био у њему, укључујући и празан.
- Померите један корак улево или удесно.
- Промените своје унутрашње стање.
Дакле, када пишете програме за сваки пар знакова или позиција, три параметра морају бити тачно описана: и - елемент из изабране абецеде А, смер померања носача ("←" на лево, "→" на десно, "точка" - без кретања) и к к је ново стање уређаја, на пример, наредба 1 "←" к 2 је постављена да "замени карактер за 1, помери главу носача улево од једне степ-ћелије и изврши прелазак у стање к 2 ".
Турингова машина: примери
Пример 1. Дајемо задатак да направимо алгоритам који додаје једну последњу цифру датог броја који се налази на траци. Улазни подаци - ријеч - знаменке цијелог децималног броја, записане у узастопним ћелијама на врпци. У почетку се уређај налази насупрот крајњем десном симболу - знаменки броја.
Одлука. Ако је последња цифра једнака 9, онда она мора бити замењена са 0, а затим додати један претходном знаку. Програм у овом случају за овај Турингов уређај може бити написан овако:
| а 0 | 0 | 1 | 2 | 3 | ... | 7 | 8 | 9 | |
| к 1 | 1 Х к 0 | 1 Х к 0 | 2 Х к 0 | 3 Х к 0 | 4 Х к 0 | ... | 8 Х к 0 | 9 Х к 0 | 0 λ к 1 |
Овде к 1 је стање промене цифре, к 0 је стоп. Ако је у к 1 аутомат фиксира елемент из серије 0..8, онда га замењује са једним од 1..9, односно, а затим прелази у к 0 стање, тј. Уређај се зауставља. Ако носач фиксира број 9, он га замењује са 0, затим се помера улево, заустављајући се у стању к 1 . Овај покрет се наставља све док уређај не фиксира цифру мању од 9. Ако су сви знакови једнаки 9, они се замјењују нулама, 0 се замјењује водећим елементом, носач ће се помакнути улијево и уписати 1 у празну ћелију. Следећи корак ће бити прелазак у стање к 0 - стоп.
Пример 2. С обзиром на низ знакова који означавају отварање и затварање заграда. Потребно је изградити Турингов уређај који ће уклонити пар реципрочних заграда, то јест, елементе распоређене у ред - "()". На примјер, почетни подаци: “) (() (()”, одговор би требао бити: “) .. ((”. Рјешење: механизам, који је у к 1 , анализира крајњи лијеви елемент у линији.
| а 0 | ( | ) | |
| к 1 | а 0 Х к 0 | (П к 2 | ) П к 1 |
| к 2 | а 0 Х к 0 | (П к 2 | ) λ к 3 |
| к 3 | а 0 Х к 0 | а 0 н к 3 | а 0 н к1 |
Наведите к 1 : ако се појави симбол “(”), затим померите удесно и идите на позицију к 2 ;
Стање к 2 : анализа заграде “(” за присуство пара се врши, у случају случајности испада “)”. Ако је елемент пар, онда се враћајте на лево и идите на к 3 .
Наведите к 3 : прво обришите симбол “(”, а затим “)” и идите на к 1 .